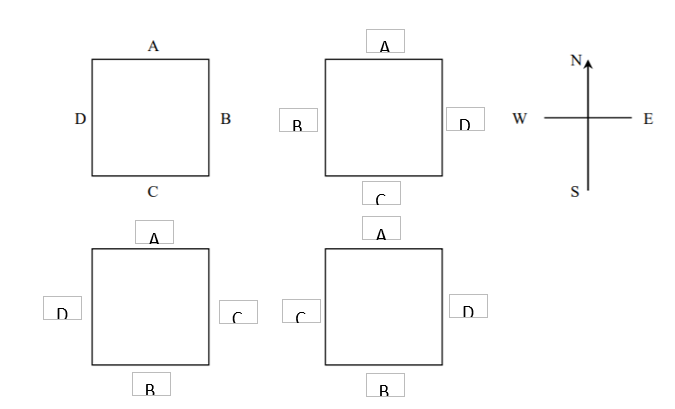
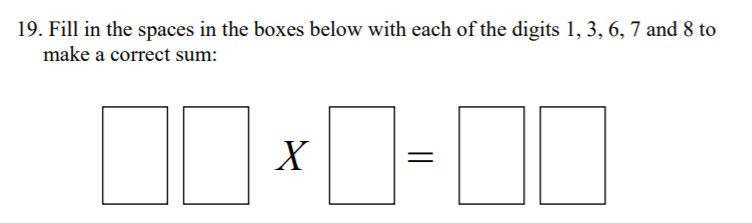121
Standard Operations Question
49
Standard Operations Question. Ensure to “borrow 1” from the 8 as you can’t do 2-3 in the Units Column
85
Standard Operations Question
36
Use Bus Stop method as the easiest approach
24
This is still difficulty 1. Its just subtraction in words
7 x 48 = 336
Standard Multiplication question…in words
£11
Standard Division question. Use Bus stop method
300
Still Standard Operations but slightly harder as its 4 numbers
53,018
The trick with numbers and being able to “easily read them” is to mark a comma every 3 digits….STARTING FROM THE RIGHT HAND SIDE of the number and working RIGHT to LEFT
£1.20
Can be done a few ways. Easiest way is to think of HCF of 750g and 1kg. This is 250g. Then to work out 250g cost and from there, x by 4
5/12
So this is a relatively common question for some schools. Find the LCM of the denominators 3 & 2. This is 6.
Therefore, x 1/3 by 2 and 1/2 by 3 which gives 2/6 and 3/6. If this doesn’t give a fraction in between the 2 fractions, then x2 for each fraction
This gives 4/12 an 6/12
This “forces” out a middle fraction of 5/12.
Note: You have to have the same denominator in order to solve this question
34
With word questions like this, just start off with one sentence at a time:
- 2/5 get off at stop 1 = 35/5 *2 = 14 passengers get off. So this leaves 21. 7 get on so this gives 28
- 28 remaining and 1/4 get off. So this is 7. Leaving 21. 13 get on so this gives 34
Many students do get confused because of the number of words and phases to this journey. However, just methodically do one sentence at a time
19
Simplest approach is to convert this to an algebra format question
So, since the number is doubled, let this equal 2x
41-2x=3
Then rearrange as per normal
-2x=3-41
2x=38
x=19
47.6
0.392
Standard Operations questions but just moving the decimals. Number of zeros in first qtn is 1, move 1 place to right. Number of zeros in second question being 2, move 2 places to left.
Multiply, move decimal to right. Divide, move decimal to left
£0
Step 1: 10% of £20 = £2
Step 2: 20% of £10 = £2
If not sure on % of an amount, use the following approach. Remember, “of” in maths means multiply
So 10/100 x 20/1. Remember to cross cancel to make the fraction easier to calculate
i) 10cm
ii) 2 inches
iii) 295cm
i) Calculate number of cm per inch. So 30cm/12.5inches = 2.5cm per inch.
4 x 2.5 = 10cm
ii) Work backwards now that you know its 2.5cm per inch
5cm/2.5cm per inch = 2 inches
iii) cm in 9ft 10 inches
9ft = 30cm (per foot) * 9 = 270cm
10 inches = 2.5 x 10 = 25cm
Total 295cm
Direction you need to turn: Anticlockwise
Angle of turn required: 60 degrees
Like prior word based questions, just break it down 1 sentence at a time:
Start at zero degrees (or think of it as 12 o’clock). 40 degrees clockwise will be to the right
70 degrees anticlockwise will take you a net 30 degrees to the left of zero
90 degrees clockwise turn from there will take you to a net 60 degrees right. So 60 degrees clockwise
5 large
13 small
Total 18 crates needed.
Question requires breaking down the words and going statement by statement
L = 12 cartons
S = 4 cartons
(5 x 12) + (20 x 4) = 140 capacity
To store 110, you would use all the large crates first:
- 5 large used = 60 cartons. So 110-60 = 50 left to find crates for
- 50/4 = 12.5. So you need 13 crates of which the 13th will have 2 cartons in there. The other 12 will be full with 4 each. So 48
78
13 x 6.
always
never
always
sometimes
The above rules are worth remembering. They help when you are checking answers. For example, if you multiply 2 odd numbers in a calculation and get an odd number as your answer, you know something is wrong. So worth remembering these
12
The best way to solve this question is with the use of Algebra. In fact many maths questions where they have someone or something being “X” times more or less than the other, Algebra comes in handy. So lets solve….
2Harsha=1Ravi
2Ravi=1Harpreet
If 42 sweets altogether, then lets work out the total number of “shares” of sweets:
4Harsha+2Ravi+1Harpreet
In the above, you start with Harpreet as being 1 share (or x if you like) and then work through to Harsha
The objective is to get to the number of “shares” to see how many portion you divide the sweets between. Its 7 times
So 42/7 means each share of sweets is worth 6.
Ravi gets 2 shares so he gets 12
seven
fifteen
A very basic question provided students read the question. Note “words” in bold. All words in bold should be taken note of in any question
i) 10am 31st January
ii) 1pm 1st February
Like prior questions, work through this question one step at a time.
i) If its 11pm in the UK on 30th January and Australia is 11 hours ahead, then one way is to add 12 hours to 11pm and take 1 hour away. So the time in Australia will be 10am. Its then the following day there so its 31st January
For number of days in the month, remember the knuckle test.!
ii) Its easier to break this down into 2 phases. Start with the time in Australia when Matilda leaves the UK:
She leaves at 10am 31st January.
Then add on the flight time of 27 hours which will be 1 day + 3 hours
So in total it will take you to 1pm on 1st February
Try and do one element at a time. Students who try and add 27 hours straight onto 10am make mistakes. So breaking it down into 1 day and then separately 3 hours, makes it easier
i) 1 burger £0.99
1 chips £1.20
1 coffee £0.65
Total £2.84
Do your workings neatly by aligning the columns for each digit
ii) Change £5.00
– £2.84
= £2.16
4 coins therefore being £2 coin, 10p, 5p, 1p
iii) 3 Sausages £1.35 (£0.45 x 3)
Meat Pie £2.20
Drink can £0.35
Total £3.90
iv) £50 – £44.40 = £5.60 spent
2 Meat Pies £4.40 (£2.20 x 2). Leaving £1.20 to spend
1 Coffee £0.65
1 Tea £0.55
Total £5.60
The above is by some trial and error. It is worth adding in the larger ticket items first. ie the Meat Pies. Then understanding where that leaves you. The answer should then be clear as being 1 coffee and 1 tea
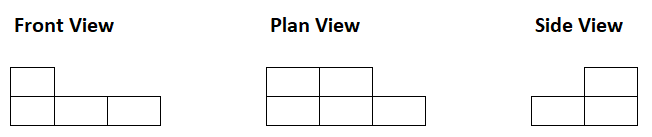
These types of questions are good practice for Non Verbal Reasoning and particularly cube related shape questions which are common.
i) 0800
The best way to read tables is always to read them horizontally and vertically. Use a ruler if needed to ensure no misalignment in reading
ii) 36minutes
Read across from 0727 Radlett until you align and then move down to the City in the same column
iii) 12minutes
Firstly evaluate St Albans to West Hampstead 0722 which arrives West Hampstead 0745. 23 Minutes
Secondly, similar for 0658. Arrives West Hampstead 0710. 12 Minutes
Work out difference
iv) 0728
Work backwards. Look at last train to get to the city before 0800 which is the 0755. Then work vertically up to see time it leaves St Albans
v) 01719
Work backwards again on this:
0855 train she needs to catch. Less 30 minutes check in means 0825. Less 10 minutes platform change means 0815. So the train arriving before 0815 at St Panceas is the 0812 train. She therefore needs to get the 0744 from St Albans
Less the 25 minute walk means that she should leave home at 0719
Completed blanks in the following order
81-25=56
14×4=56
They are the same. (NOTE: This is a nice trick to remember). Follow the example guideline.
(552+448)x(552-448) = 1000 x 104 = 104,000
(8.5+7.5)x(8.5-7.5) = 16 x 1 = 16
(19/37+18/37)x(19/37-18/37) = 37/37 x 1/37 = 1/37
(25001+24999)x(25001-24999) = 50,000 x 2 = 100,000
NOTE: The above is a great approach to remember for future questions.
i) 10 miles
ii) S to B to F to E to D to T
The thing to note here is that the map is not drawn to scale so extra attention has to be paid to the miles between different points
iii) 40 minutes
Time = Distance/ Speed. So substituting into the formula, Time = 10/15 which = 2/3 of 1 Hour (10/15 x 60). So thats 40 minutes
iv) 8 minutes
The revised route is S-B-C-T. So an extra 2 miles
This means 12/15 of 1 hour so 12/15 x 60 = 48 minutes
Difference being 8 minutes
a) 28.7 (per formula)
b) Overweight
c) 28.4 (per formula)
d) 132.3kg (per formula)
e) 8.6kg ( 61.6 – 53)

a) 16
b) 24
(However many people there are, permutations are each number x each number. So for example if there are 3 people, possible permuations are 1x2x3 =6. For 4 people, its 1x2x3x4)