Geometry

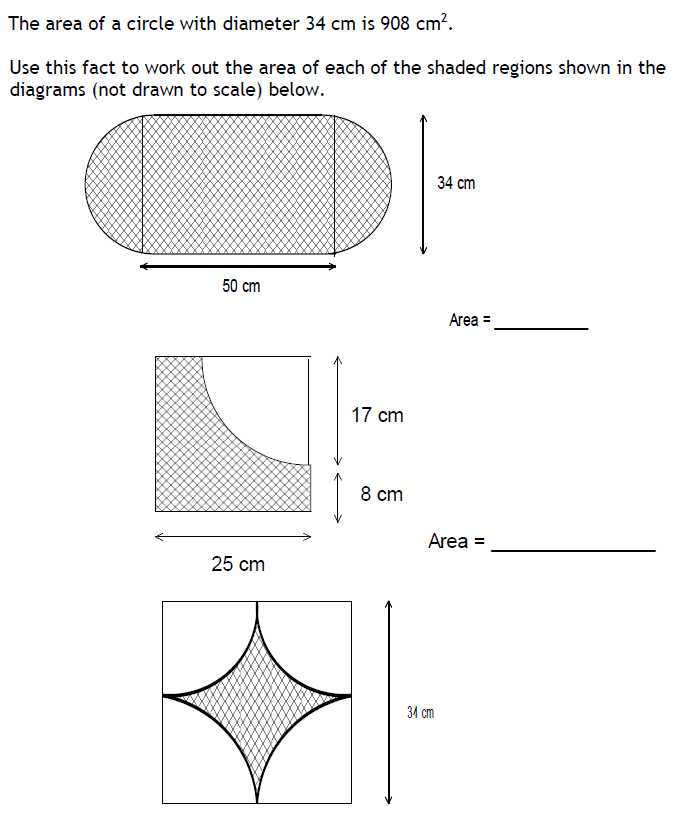
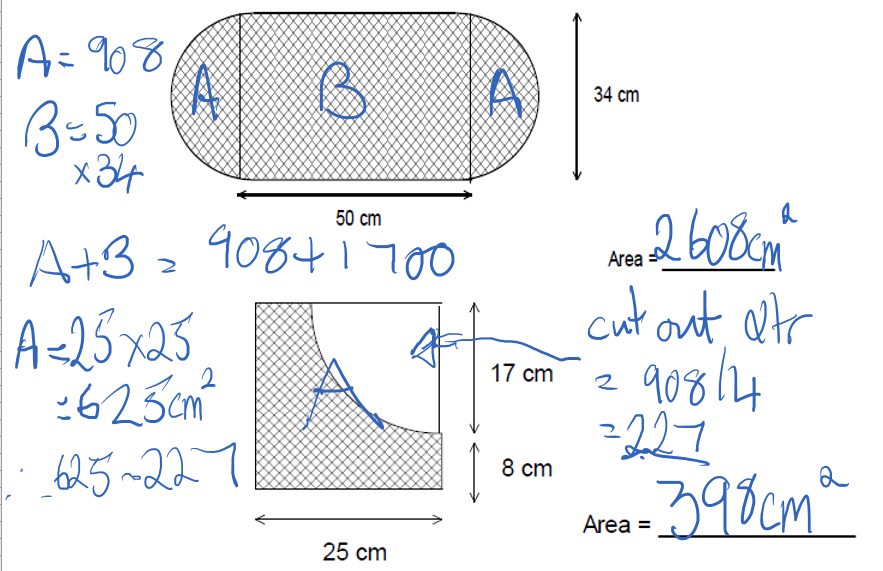
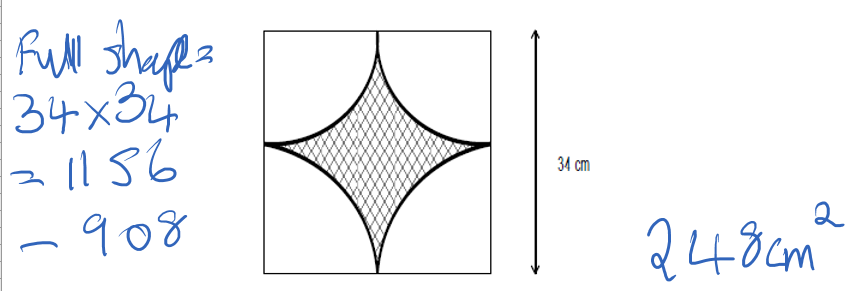
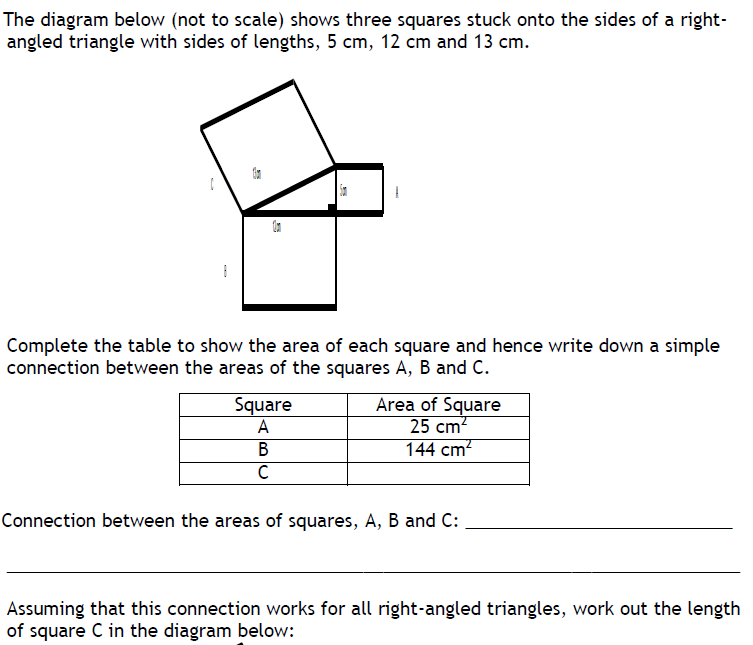
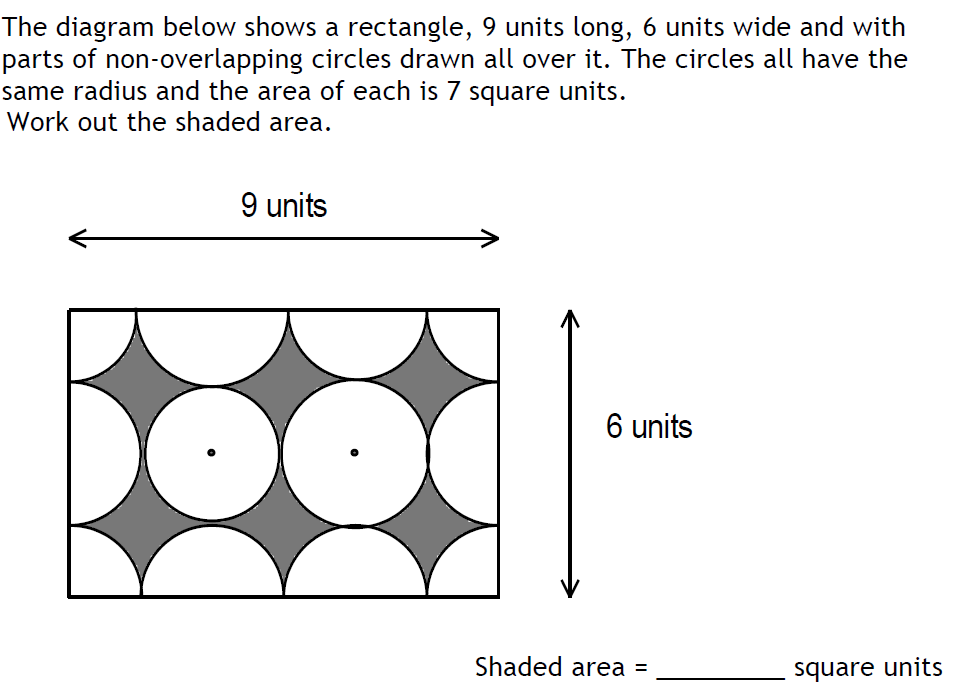
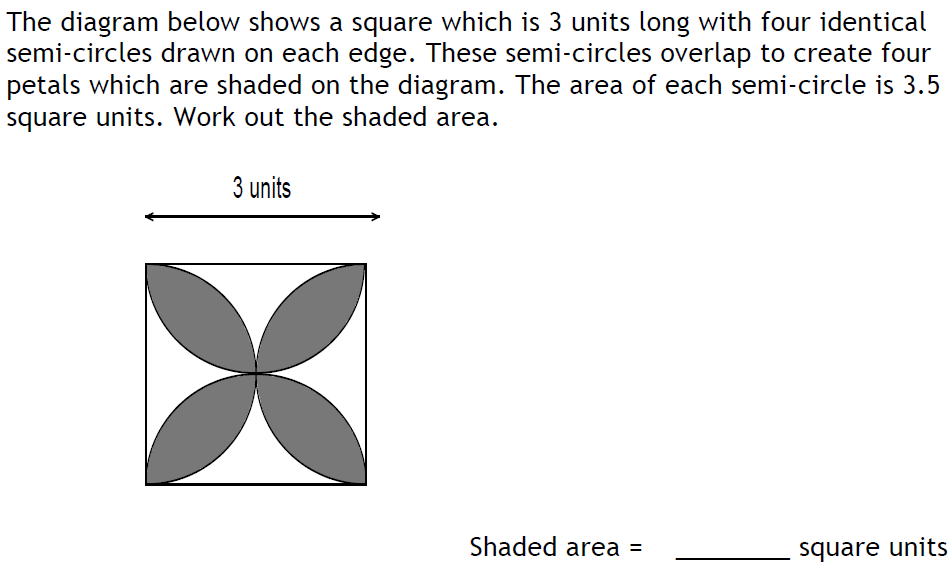
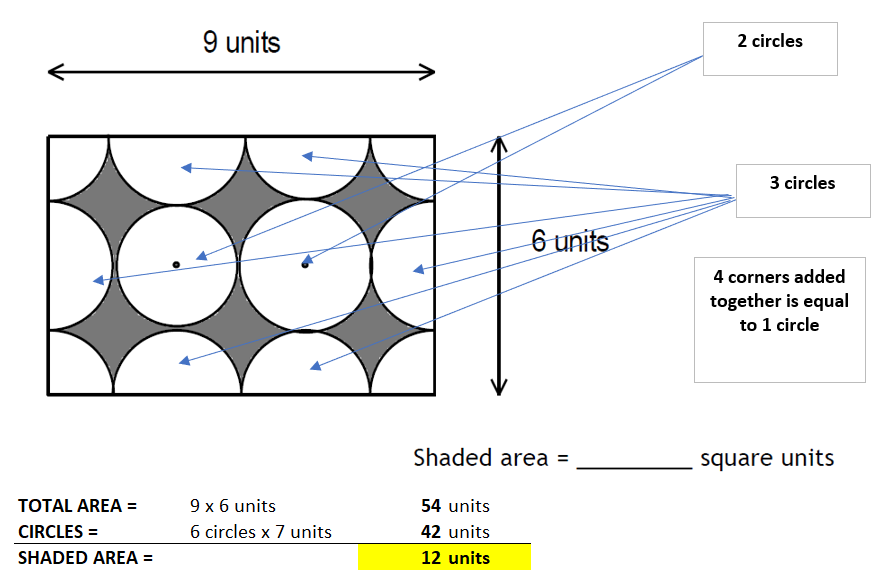
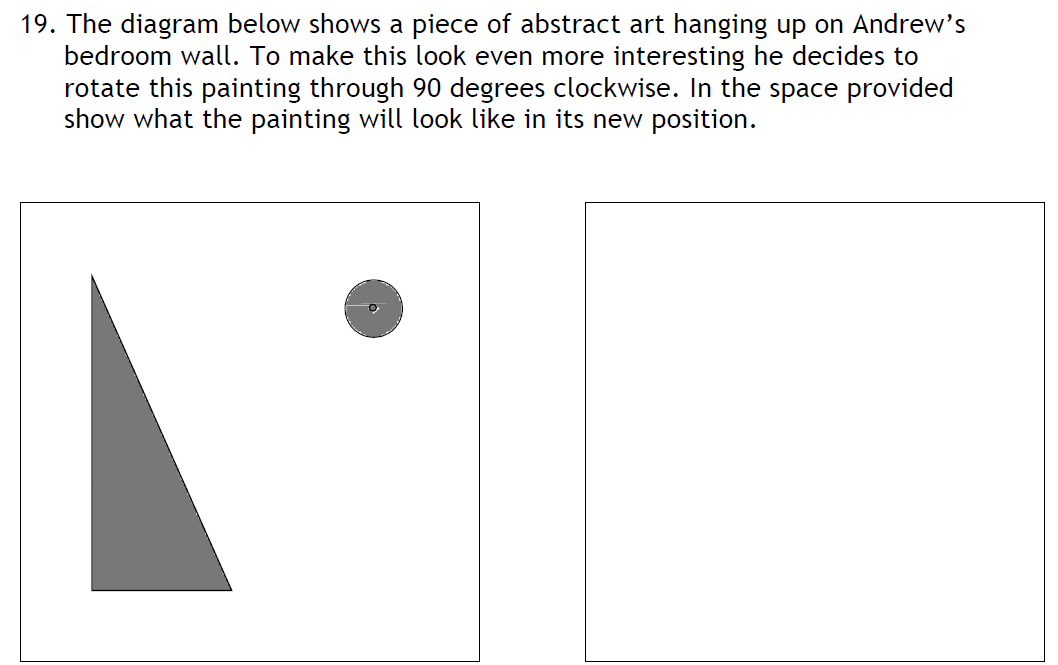
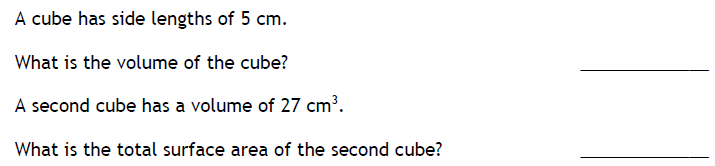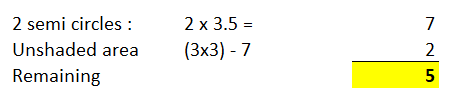1 and 4

8m

1. Area is LxW
2. So working backwards, 72=9xW
3. Rearrange. W=8

72 stickers

1. 80/10 = 8
2. 45/5 = 9
3. 8 * 9 = 72

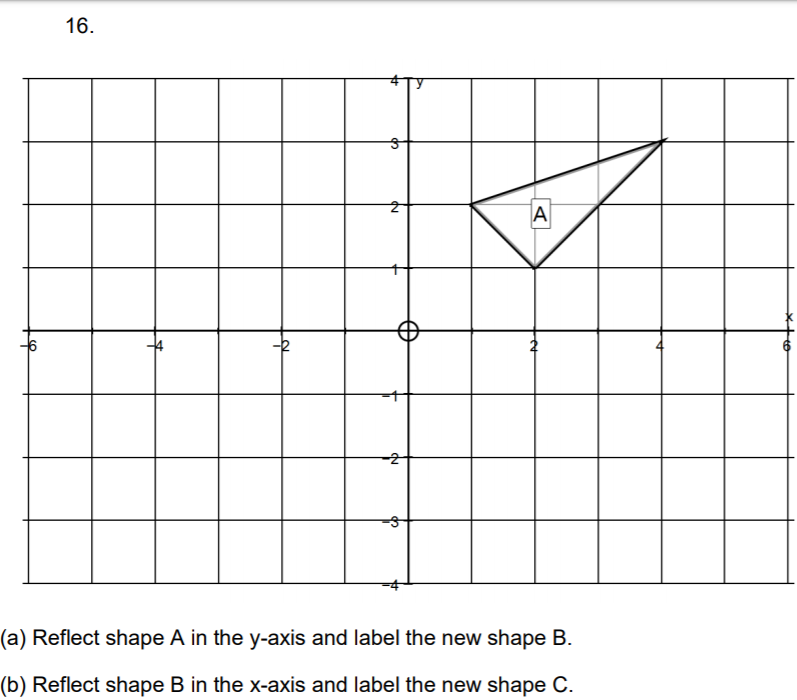
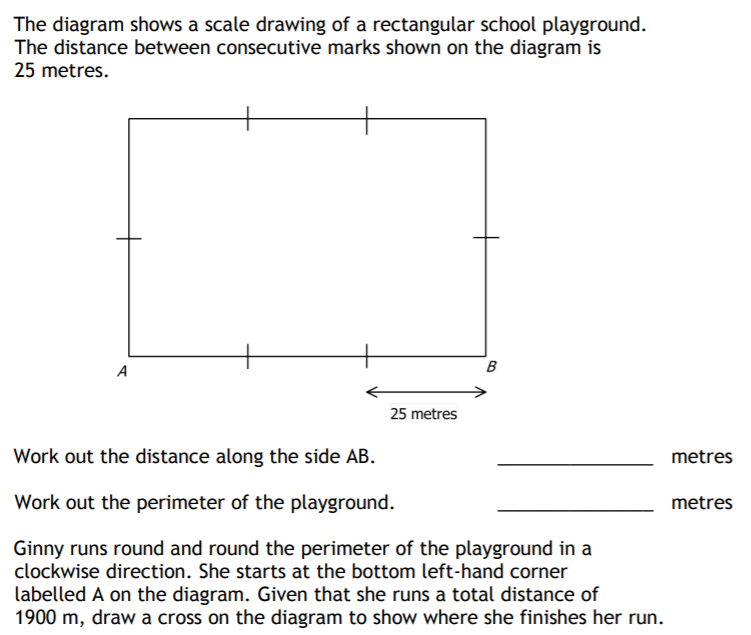
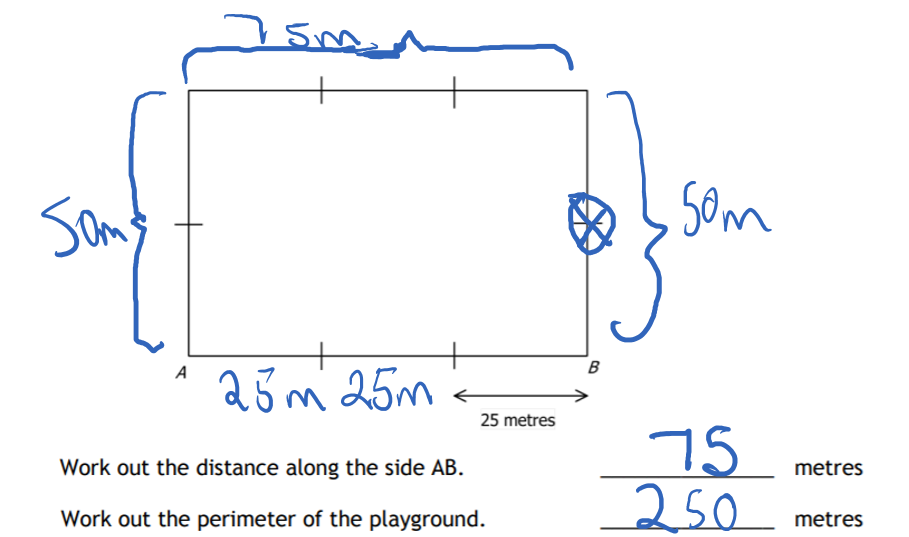
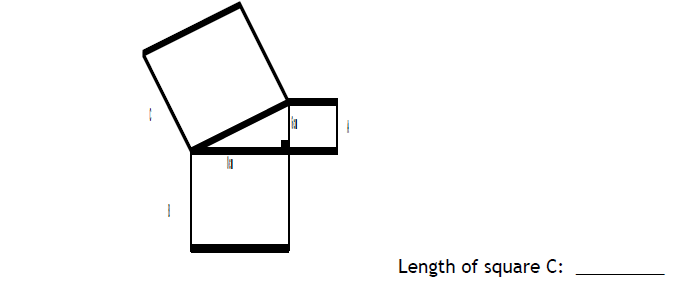
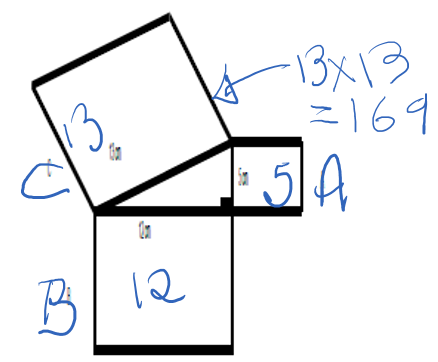
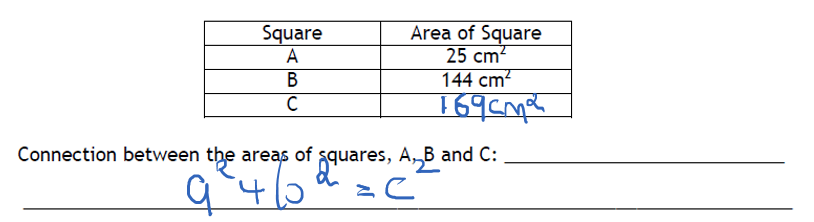
A

36cm² as area means sides must be 6cm long each.

Therefore, total is 24cm

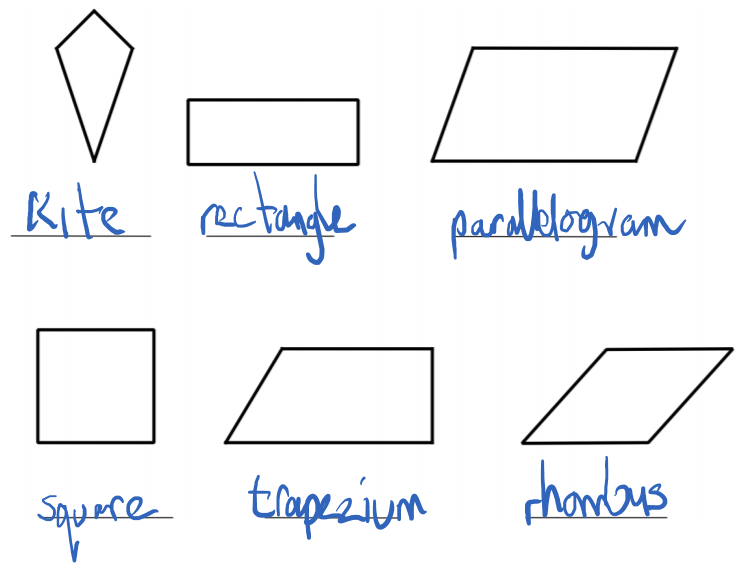
B

1. 180 – 25 – 107 = 48

44 stickers

1. Use division as a starting point
2. So 60/15 = 4
3. 55/5 = 11
4. Multiply the 2 to get 44 stickers

c) 55

Notice the pattern and sequence. 1 gives 4 gives 9 gives 16. So a change of 3, 5, 7, 9 etc. Apply this pattern

a) See below

b) See below

c) 40

10 x 4

d) 5,050

This can be done with the following calculation

(100×101)/ 2 = 101 x 50 = 5,050

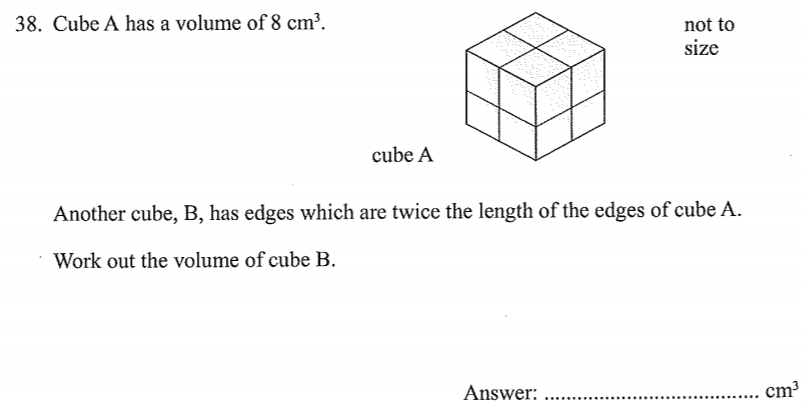
64cm³

The volume of Cube A is 8cm³. So this is 2x2x2. For 64cm, think of cube numbers. So 2x2x2 = 8. 3x3x3 = 27. 4x4x4=64

So double the side of Cube A is 4 so its 64cm³

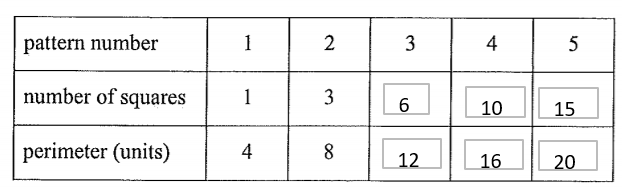
a) 48cm

See labelling below

b) 108cm²

Area = WxL. 6×18

c) 18

In 18cm across, she can fit 6 (18/3). Given its 6cm tall, she can fit 3 high. So in total 3 rows each with 6 in each row  18

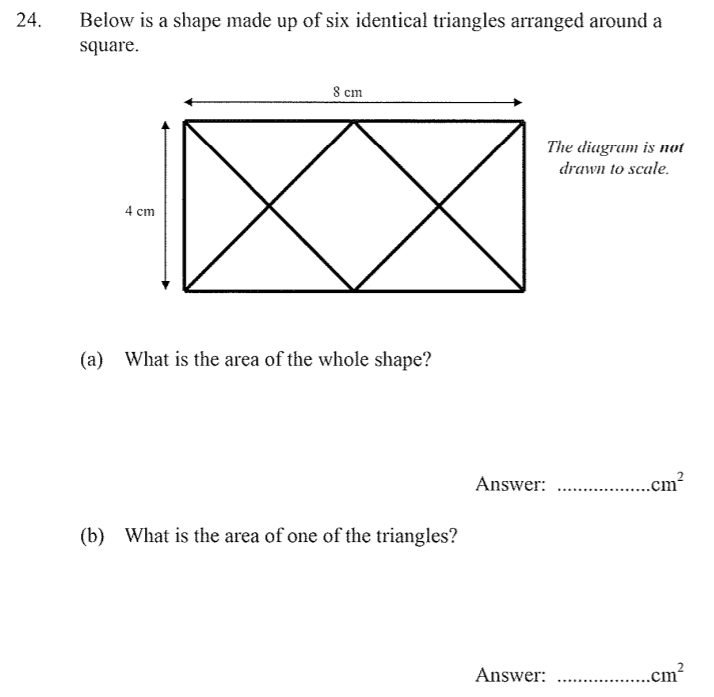
a) See below

Its 2 4×7 triangles that have been transposed from the original question

b) See below

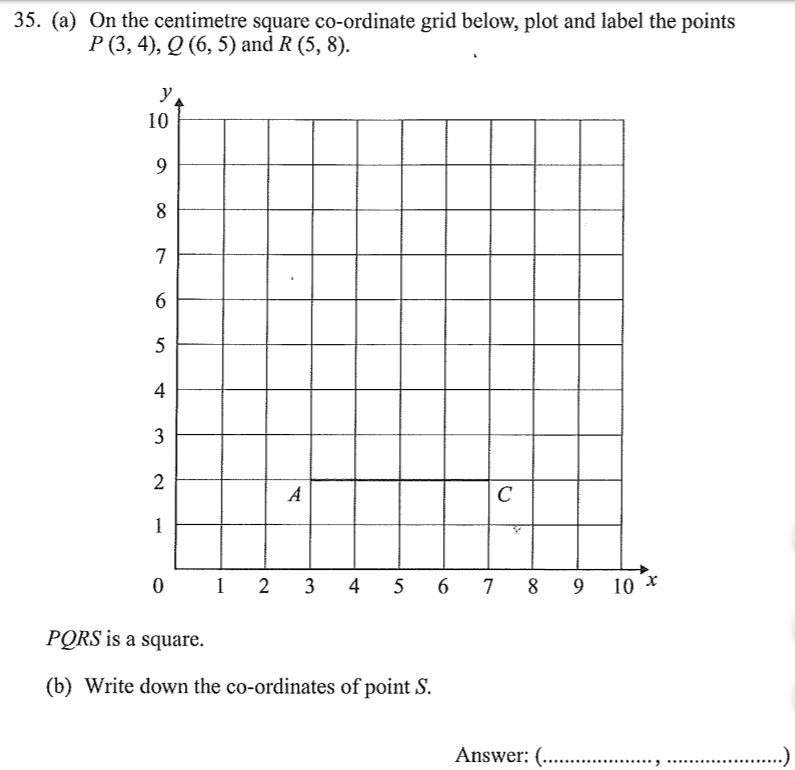
a) See below

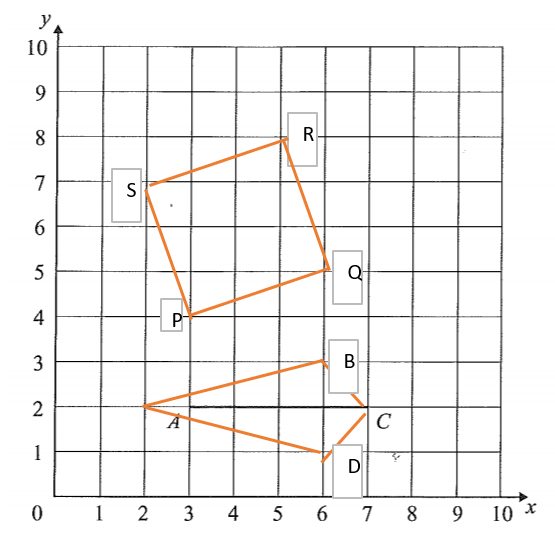
b) (2,7)

c) See above for drawing

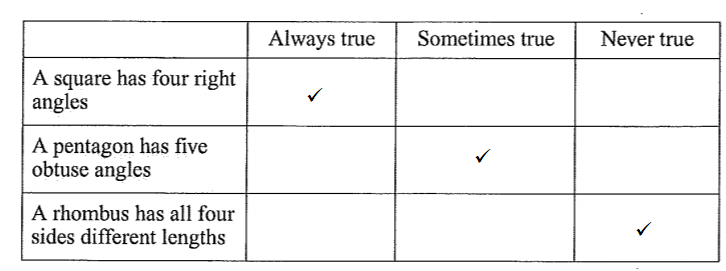
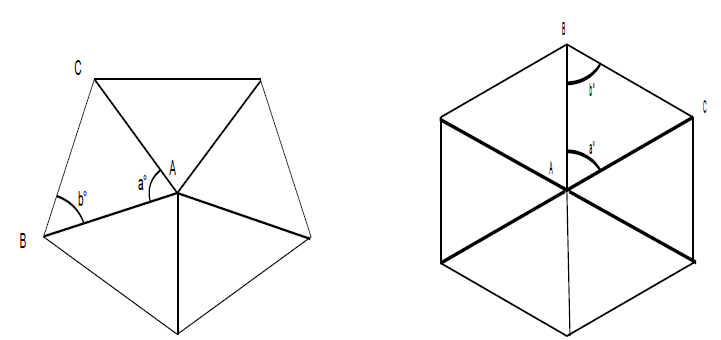
A pentagon can have 5 obtuse angles but not always has to be the case

25cm²

If perimeter is 20cm, each side is 5cm

Therefore, the area is 5 x 5 = 25cm²

5/8ths is shaded

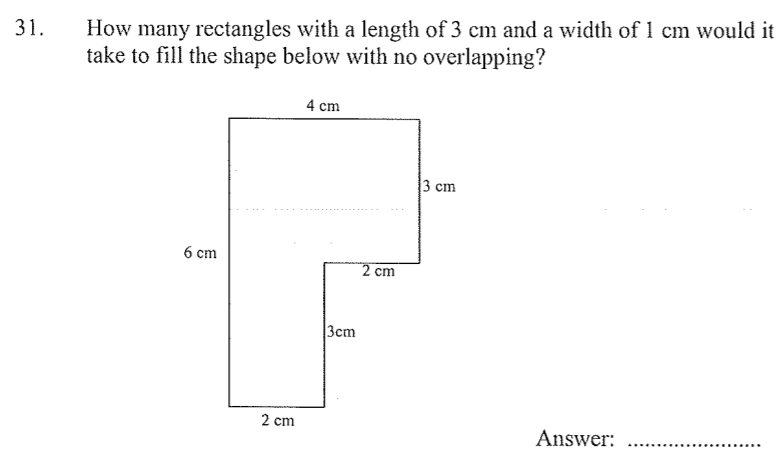
6

A is 6 x 2. Given we have a 3 x 1, we can fit in 4 rectangles into this side

B is 3 x 2. Given we have a 3 x 1, we ca fit in 2 rectangles into this side

a) 9cm

Perimeter of 36cm . 4 sides. So 9cm per side (36/4)

b) 81cm²

9×9

a) 32cm²

Area of a rectangle = LxW

b) 4cm²

8 triangles altogether = 1/2 LxW

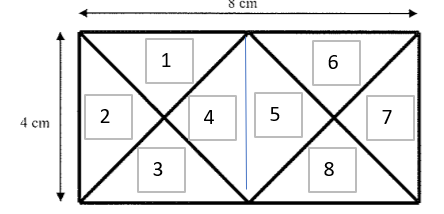
c) 8cm²

4 and 5 in the above

d) 12

6 small triangles from 1,2,3,6,7,8

4 medium triangles from (1,2) , (2,3), (6,7), (7,8)

2 larger triangles from (1,4,5,6) and (3,4,5,8)

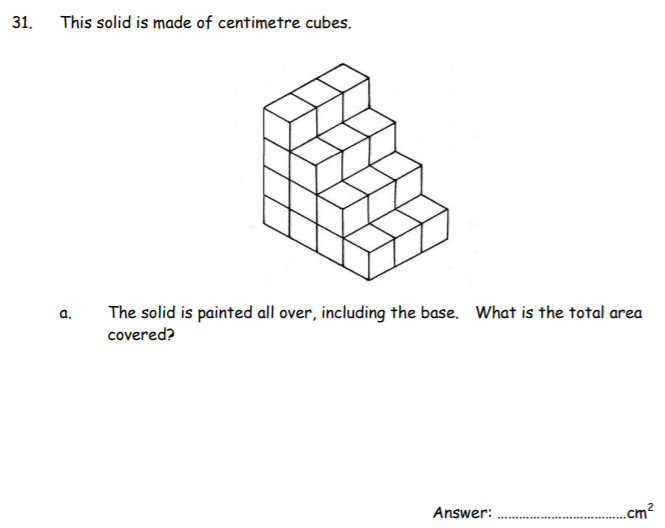
a) 68cm²

1. Firstly we need to count the number of cubes. This is equal to 30
2. For the 30 cubes, these can be split as follows:
   1. 1. There are 12 cubes….the steps if you look from South East to North West angle. 2 sides visible so thats 24 in total
      2. Next the cubes at the side looking from South West to North East angle. There are 6 visible cubes and in total, 10 surfaces. This is the same on the other side so its 20 visible sides in total
      3. Finally, 6 cubes have 4 sides showing
      4. Total therefore is 68 sides showing

b) 3 cubes left

Easier than part a for sure!. 30 cubes in part a and 27 in part b

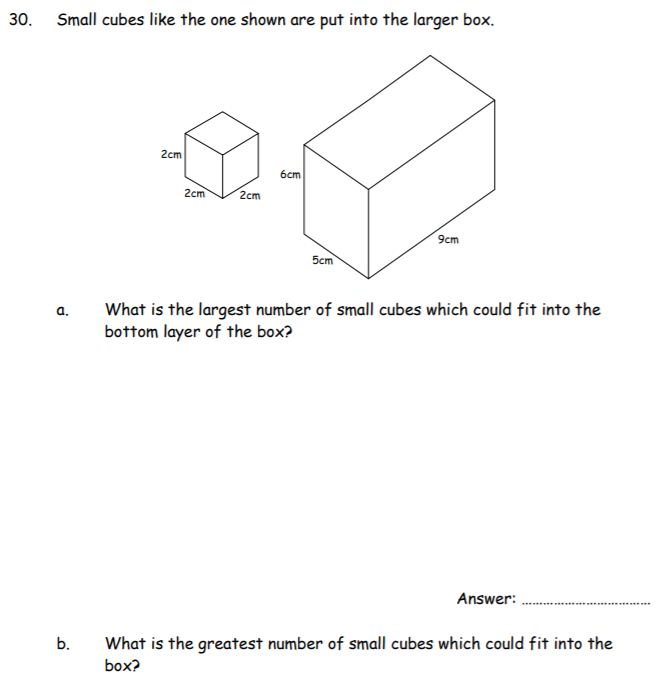
a) 8 small boxes in the bottom layer

1. Given the height of the cube is 2cm, a total of 3 high can fit in the larger box
2. The bottom layer of the larger box would therefore occupy 2 x 5 x 9 = 90cm³
3. But some space would be left around the base. Below is an aerial view

b) 24 small boxes

1. As mentioned above, 3 layers in total
2. Therefore 8 x 3 =24
3. A 1 x 1 would be left as empty space as you would not be able to break a small box and fit it into the sides

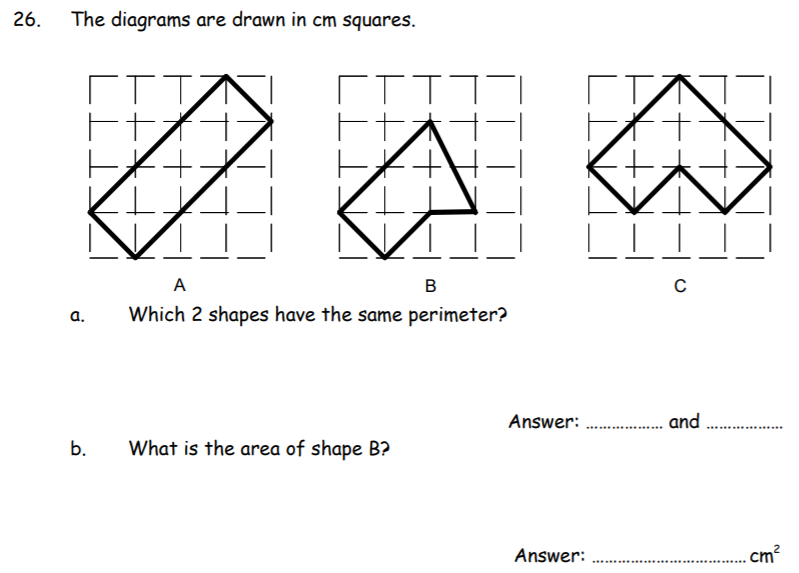
a) A & C. Both have a perimeter of 8

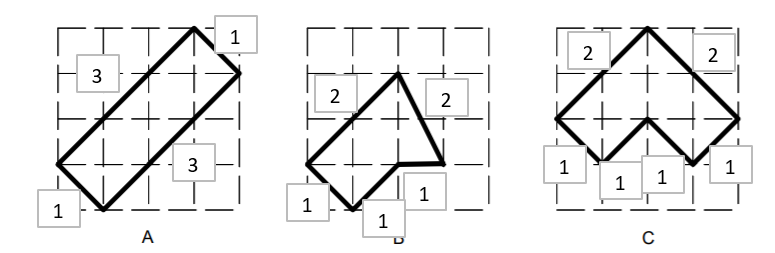
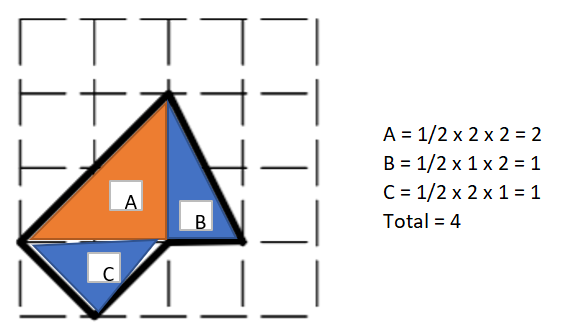
b) 4cm²

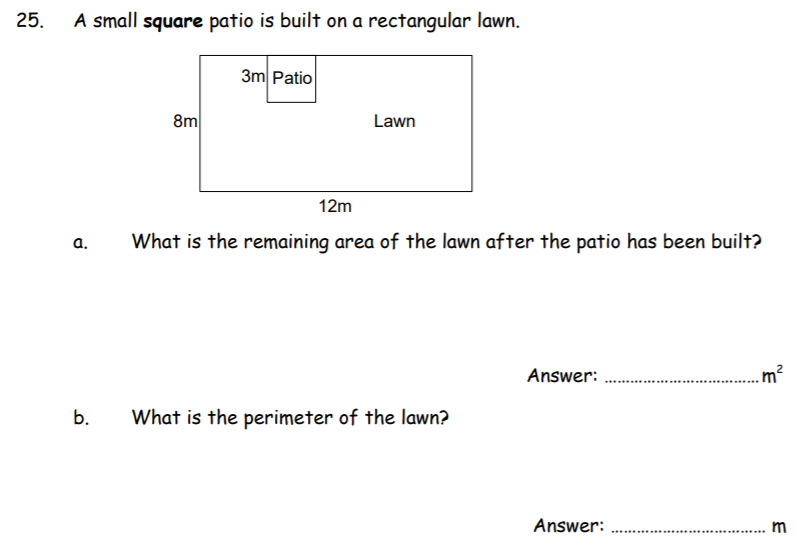
a) 87m²

1. The area of the lawn is 96m² (12 x 8)
2. The patio will take 3 x 3 = 9m²
3. Therefore, the remaining area of the lawn is 96 – 9 = 87m²

b)  40m

1. The perimeter of the lawn is 2 x (12 + 8) = 40m

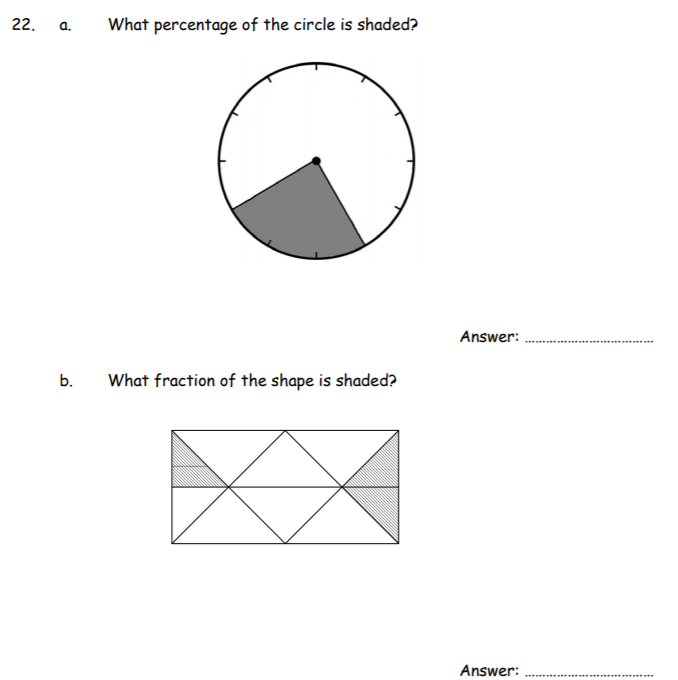
a) 25%

1. Firstly count the number of segments. There are 12 segments
2. 3 of the segments are shaded
3. Therefore in total, 3/12 are shaded = 25%

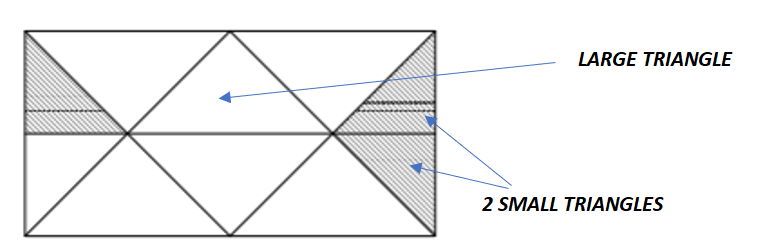
b) 3/16

1. Each Large Triangle is equivalent to 2 small triangles
2. There are 3 small triangles shaded out of a total of 16

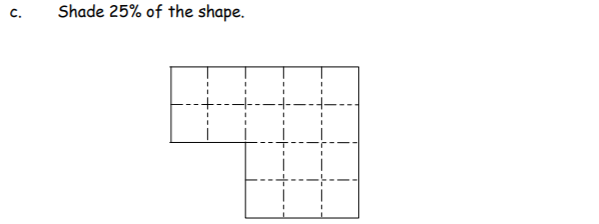
c) See below

1. 16 squares altogether
2. 4/16 = 25% shaded

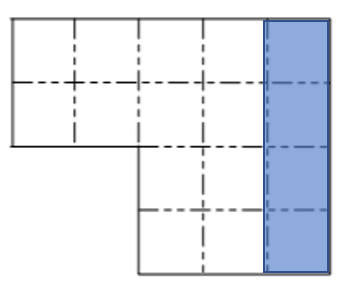
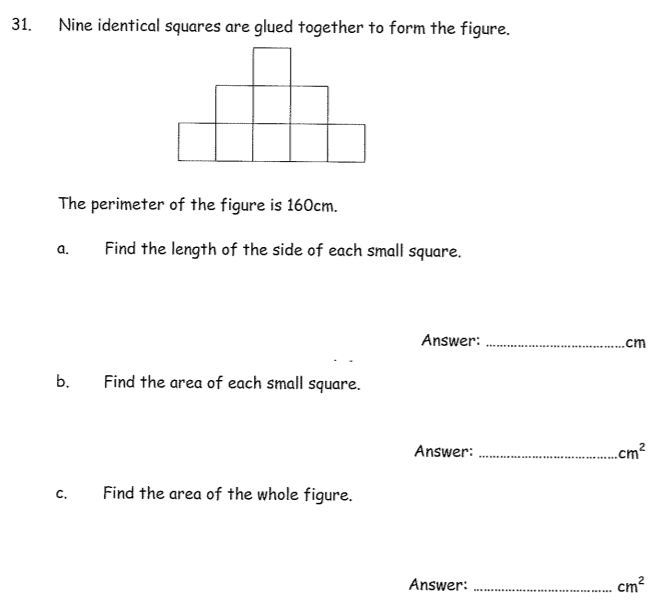
a) 10cm

1. This is a classic question and worth remembering the process to tackle these.
2. Perimeter is based on 16 sides.
3. Given perimeter is 160cm, each side is 160/16 = 10cm in length

b) 100cm²

10×10

c) 1600cm²

If each Square is 100cm², area of whole figure is 16 x 100

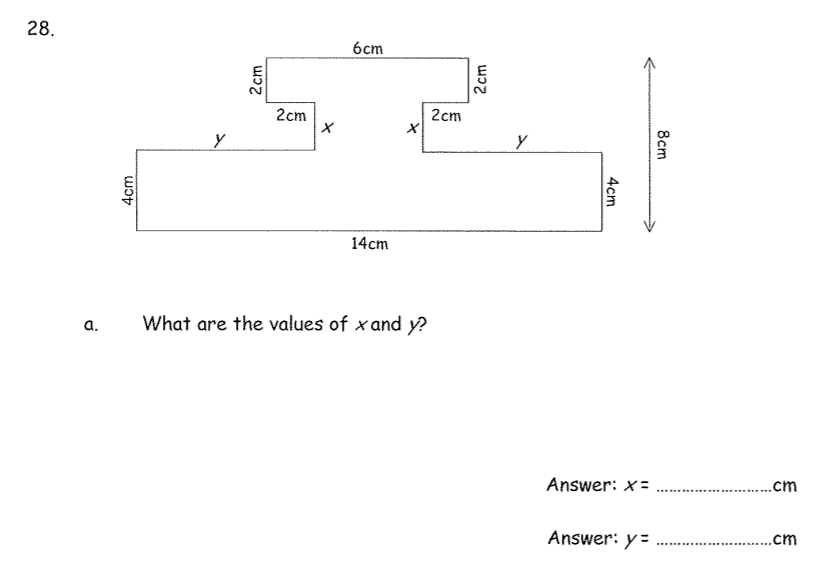
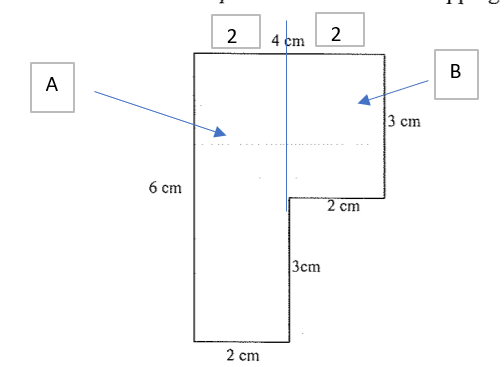
a) x = 2cm, y = 6cm

x = 2cm (8cm – A – B)

y = 6cm (14cm – E)/2

b) 52cm

Perimeter starting at point A = 2+6+2+2+2+6+4+14+4+6+2+2

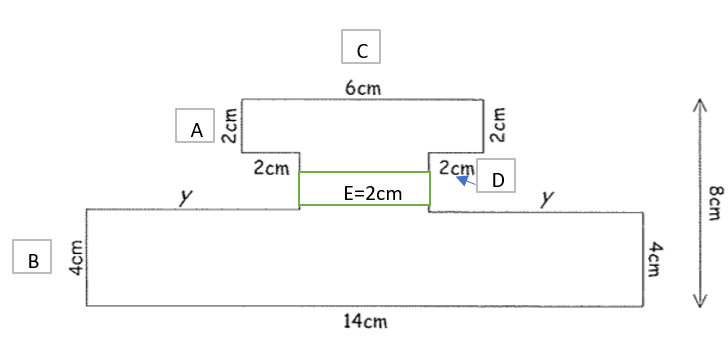
c) 72cm²

Area = (14×4) + (2×2) + (6×2) = 56 + 4 + 12

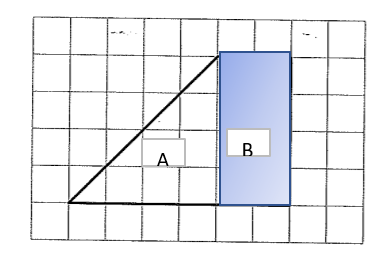
16units²

1. Break it down into 2 parts
2. Shape A = 1/2 x Width x Height. So this is 1/2 x 4 x 4 = 8
3. Shape B = 2 x 4 = 8

5 cubes

1. Tall Cube. Number of cubes is W * L * H. This equals 2 * 2 * 8. = 32
2. Small Cube. Number of cubes is W * L * H. This equals 3 * 3 * 3 = 27

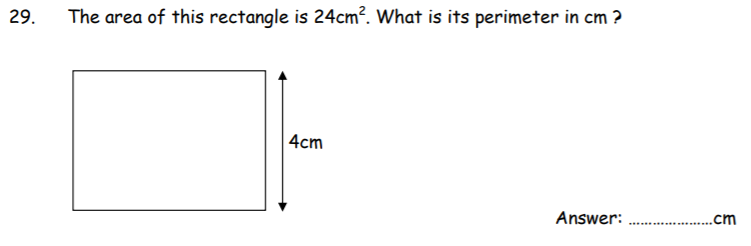
20cm

1. Very Standard style question where you are given the area and have to work out the perimeter.
2. x * 4 = 24cm² would give the area. So re-arrange this. Where x = Length. 4 is Width
3. 24/4 = x
4. x = 6
5. So if x = 6, the solution is [(2 * 6) + (2 * 4) ]

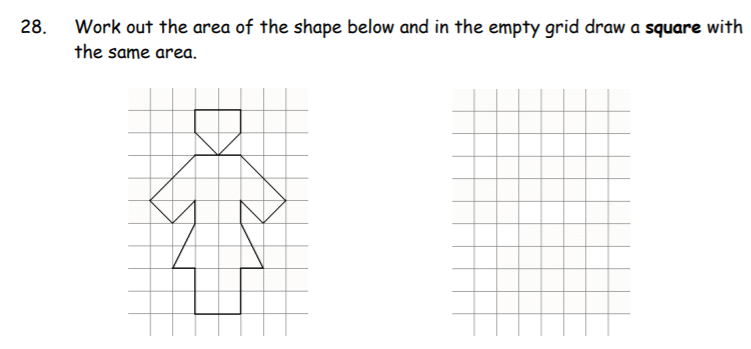
1. Area of the shape is 18 full squares + 7 other squares from partially filled squares
2. Total area = 25 squares

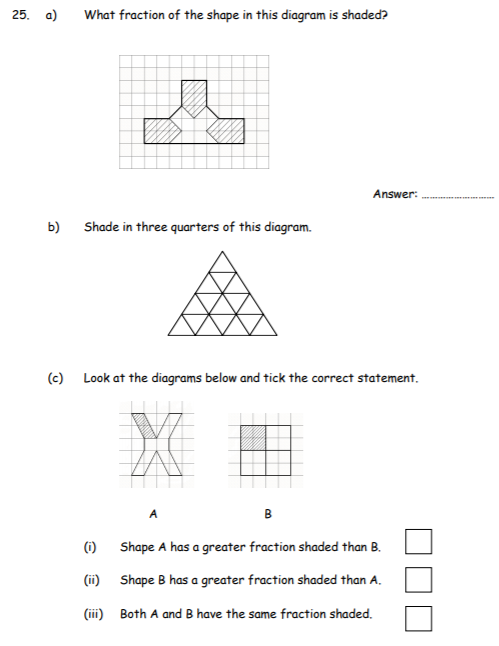
a) 15/23

1. Consider total area of shape = 23 squares
2. Shaded area is equal on all 3 sides. Each side has 5 shaded squares
3. Total shaded area = 15/23

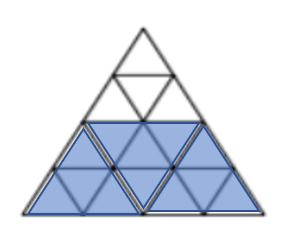
b) See below

1. 16 triangles in total
2. 3/4 shaded = 12/16 shaded

c) i) Shape A DOES NOT have a greater fraction shaded than Shape B

1. Shape A – 10 squares altogether. 2/10 shaded = 1/5th shaded
2. Shape B – 16 squares altogether. 4/16 shaded = 1/4 shaded

c) ii) Shape B DOES have a greater fraction shaded than Shape A. (Inverse of the statement for i). So this is the right statement

c) iii) This  is NOT CORRECT

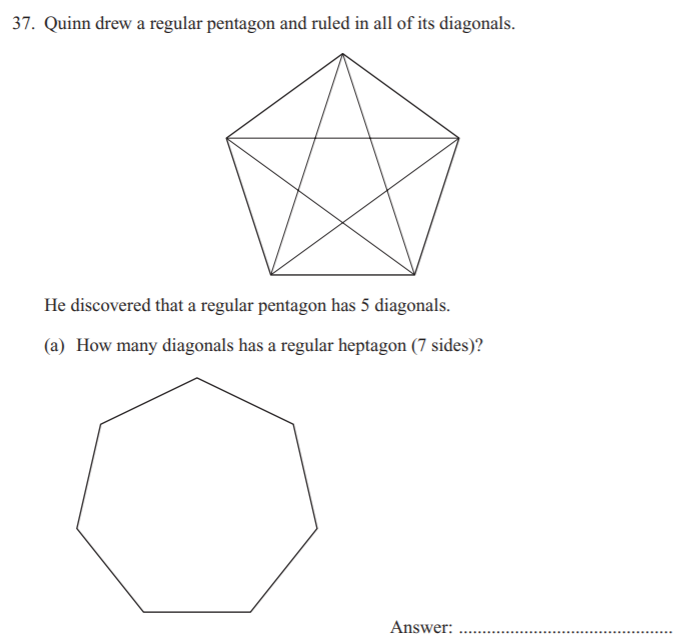
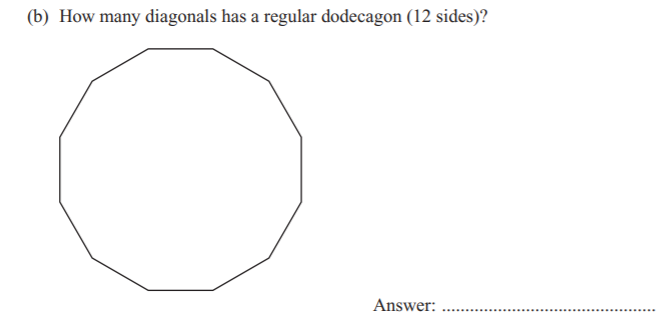
a) 14

A diagonal is a line that connects two non-adjacent corners. All polygons, except for the triangle, have a number of diagonals. The formula to find the number of diagonals is n(n – 3)/2, where n is the number of sides the polygon has

b) 54

So using the above formula, 12(12-3)/2 = (144-36)/2 = 108/2

a) 21cm

6 x 3.5cm = 21cm

b) 63cm

Pattern 2 has 3 sides per hexagon on the outside. So its 18 sides altogether. 18 X 3.5

c) 19 hexagons

Pattern 3 will require 12 additional hexagons. 1 hexagon will cover 2 of the outsides and the next one 1 outside of pattern 2. And so on. So it will be 1+6+12 (Pattern 1 + Pattern 2 + Pattern 3)

d) 105cm

30  sides will be showing for Pattern 3 on the outside. So 30 * 3.5

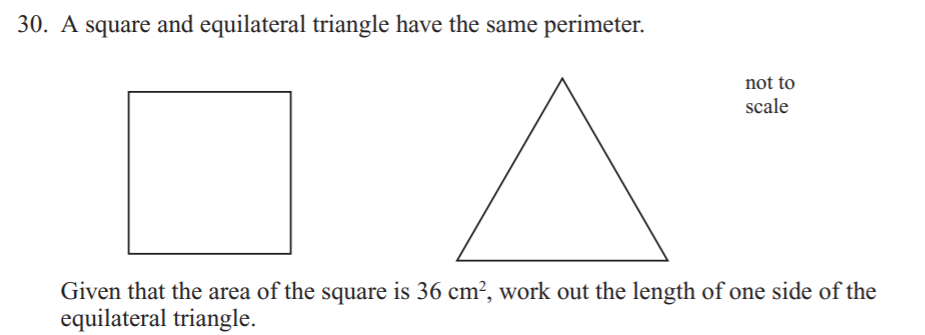
8cm

If Square area is 36cm², then each side is 6cm. Perimeter is therefore 24cm. Given the perimeter of the triangle is the same, each side of the triangle must be 24/3 = 8cm

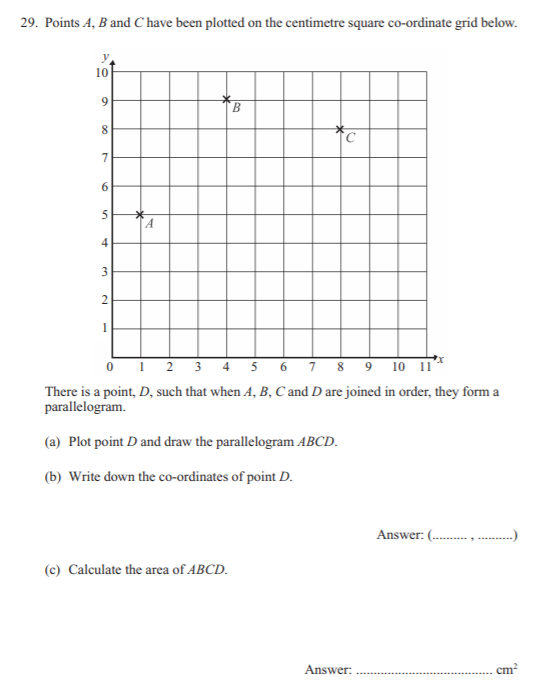
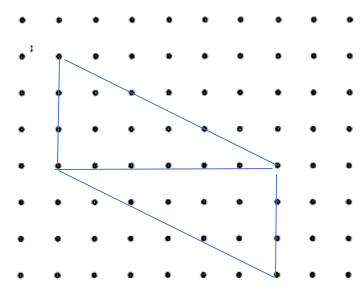
a) See the diagram below

b) (5,4)

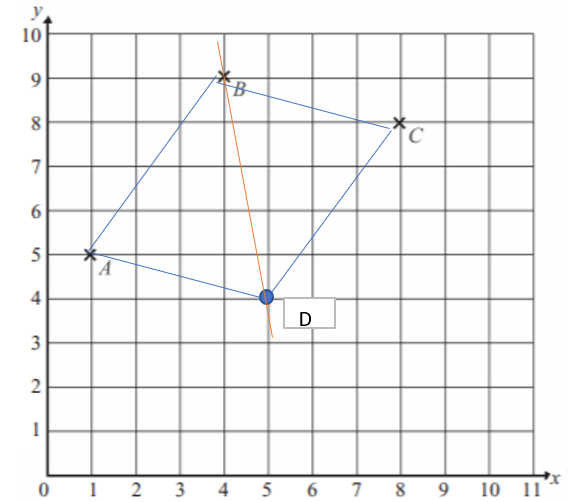
c) 17.5cm²

Area: Point A (1,5); B (4,9); C (8,8); D (5,4)

2 Triangles in effect with ABD & BCD.

ABD Area – A to midpoint BD is 3.5. Base is 5 for B to D (co-ordinate for Y axis for B of 9 less co-ordinate for D of 4)

So area of ABD = (1/2 * 3.5 * 5) =  15.75 * 2 = 8.75. * 2 as there are 2 triangles = 17.5

26cm²

Area covered in paint if all 6 cubes are dipped in paint is W*L*D = (1*1*1) * 6 sides * 6 cubes = 36

However, there are 10 covered faces. (remember to count those back to back faces as 2). So in total, 10cm²

a) 12

Area of a cube is 3 x 2 x 2 = 12 (L x H x D)

b) 84

6 x 4 x 4 = 96. Less what was used by Tilly = 84

a) 8cm²

Count the number of full squares first = 5

Then pair up the smaller squares to whole ones. The ones on the left come to 2 squares. The ones on the right that are not complete come to 1 square. Total is 8

b) See below

Note the triangle can be many different permutations. One example below

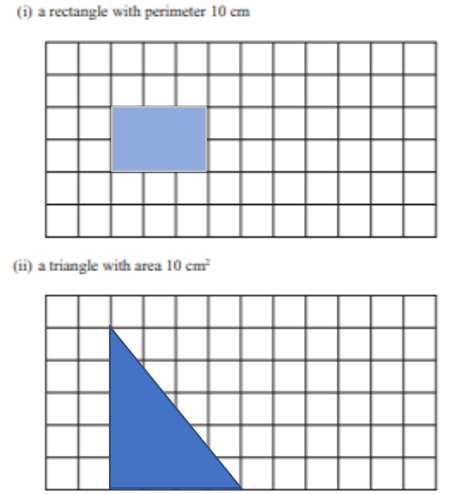
a) octagon

b) obtuse

(greater than 90 degrees)

c) i) 3.4cm

c ii) 27.2cm

34mm x 8 = 272mm

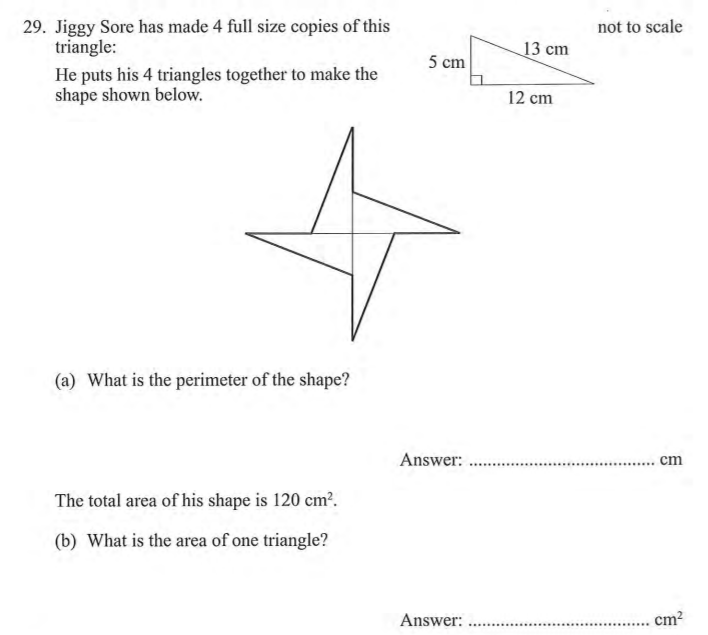
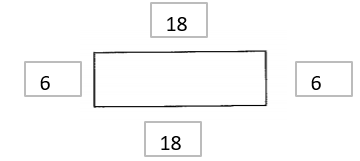
a) 80cm

Quite a tricky question so key to label like for like sides

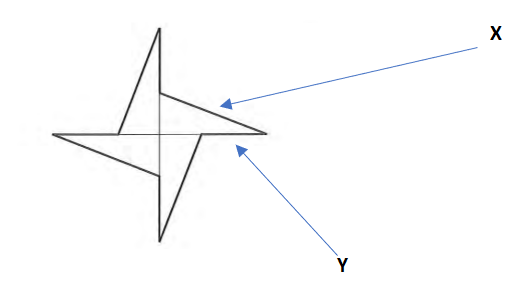
X = 13cm. There are 4 of these so thats 13 x 4 = 52cm

Y = 12-5cm (Take away 5 because the height is the central part that is not part of the perimeter. So thats 7 * 4 = 28cm

b) 30cm²

Just divide the total by 4

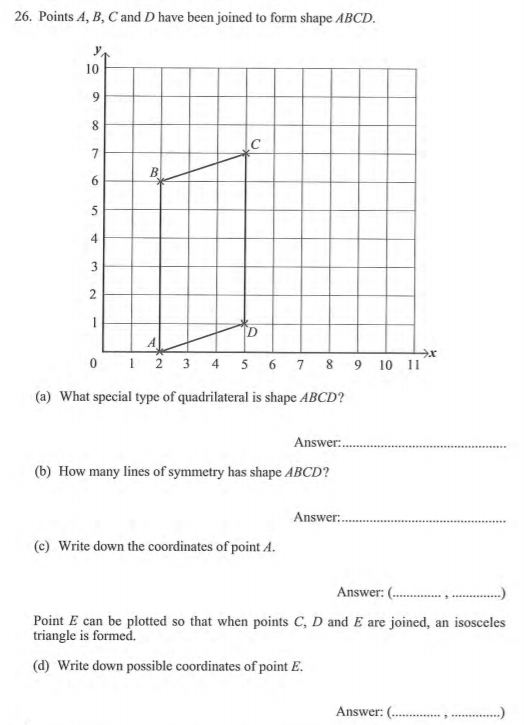
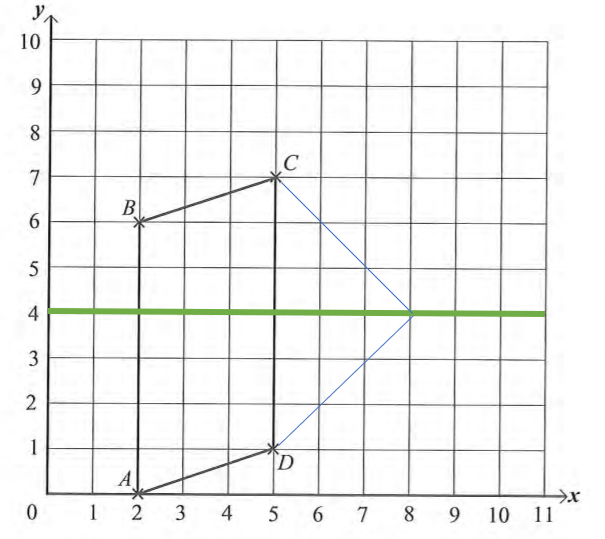
a) Parallelogram

…A rectangle pushed over sideways

b) 0

A parallelogram has zero lines of symmetry

…A square however pushed over sideways, has 2 lines of symmetry (A rhombus)

c) (2,0)

Always read X Axis first

d) See below

One example of many are below with co-ordinates below of (8,4). Provided you do not use co-ordinates of (5,5) for point E, then any replacement of the X Axis will suffice. So eg (1,4), (2,4) etc all work as does (9,4), (10,4) etc

a) 12cm²

Count whole squares first = 11

Partial half squares = 2 halves = 1

b) See below

a) b) c) See below

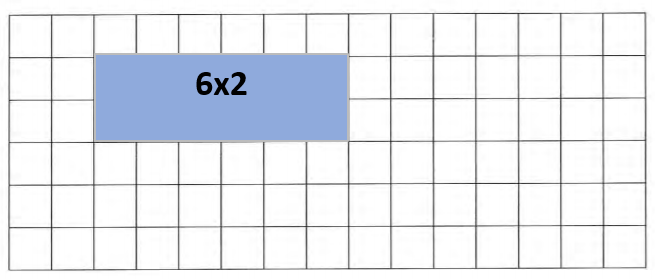
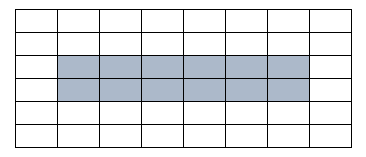
a) 12cm²

Each shaded box is 1cm x 1cm.

b) 18cm

Ensure you label each side to confirm all sides are included in the calculation

c) 6×2 rectangle drawn

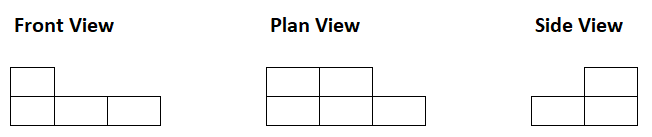
These types of questions are good practice for Non Verbal Reasoning and particularly cube related shape questions which are common.

Direction you need to turn: Anticlockwise

Angle of turn required: 60 degrees

Like prior word based questions, just break it down 1 sentence at a time:

Start at zero degrees (or think of it as 12 o’clock). 40 degrees clockwise will be to the right

70 degrees anticlockwise will take you a net 30 degrees to the left of zero

90 degrees clockwise turn from there will take you to a net 60 degrees right. So 60 degrees clockwise