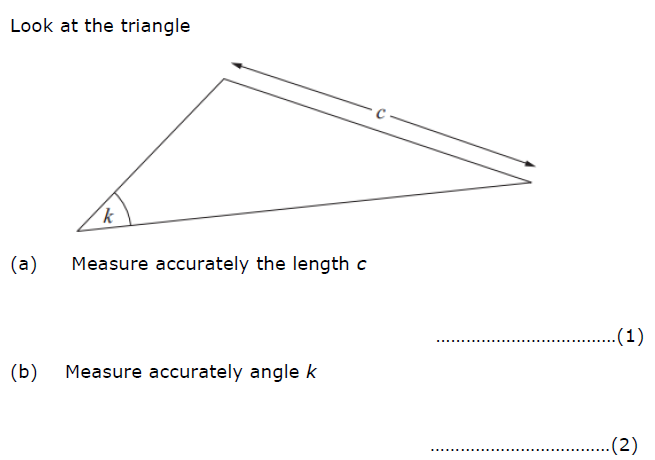
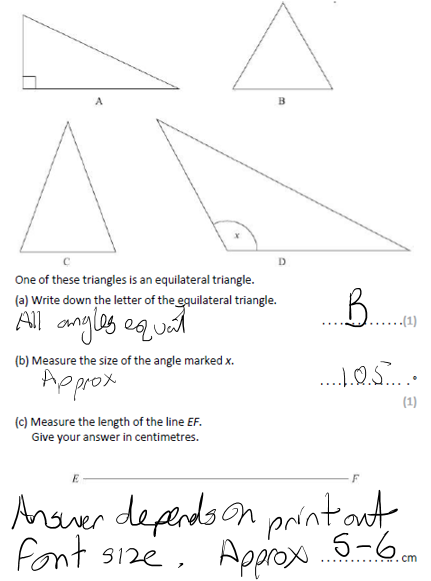
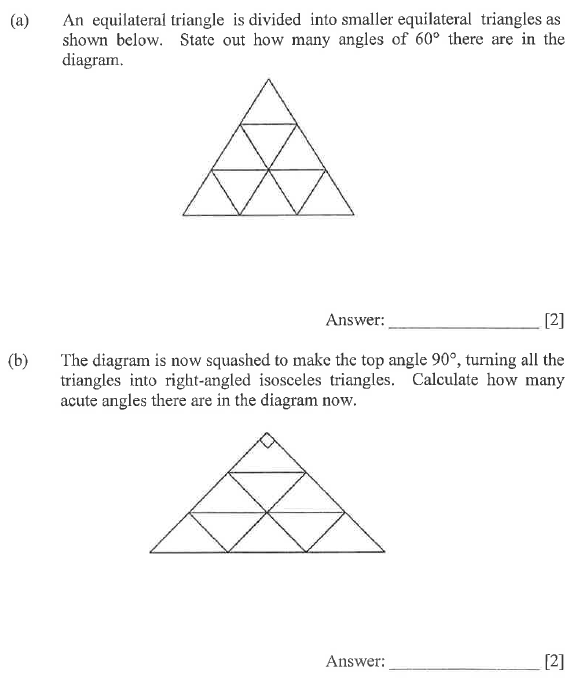
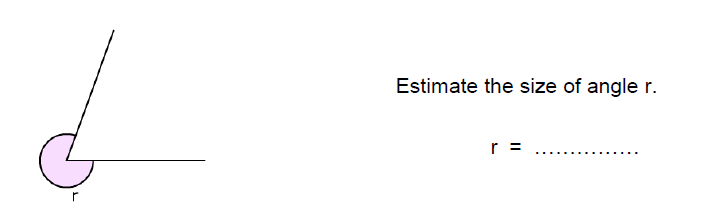a) 5cm
Length depends on whether you are looking at a print out or on screen
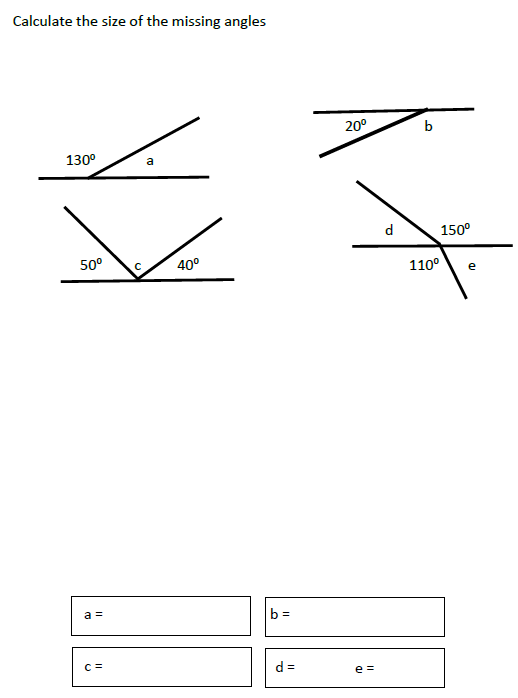
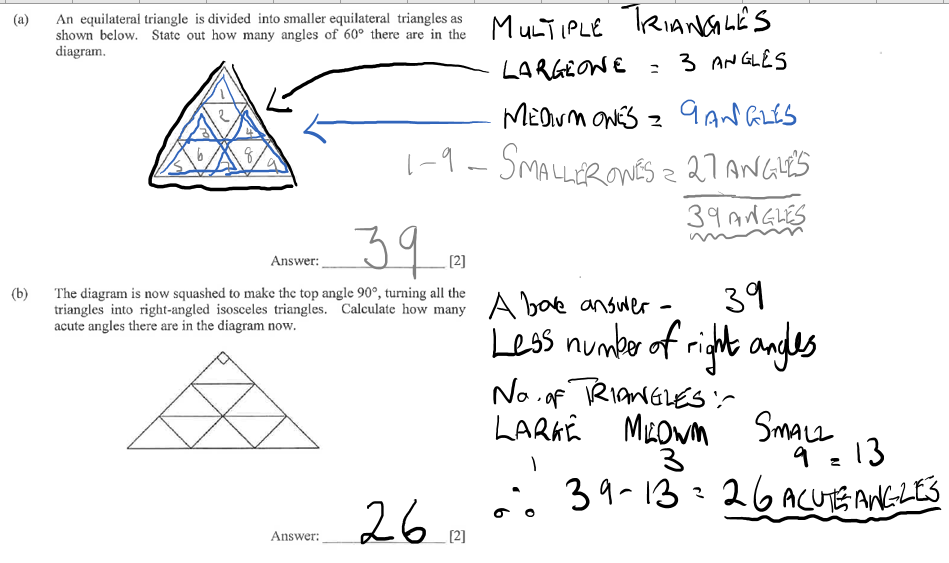
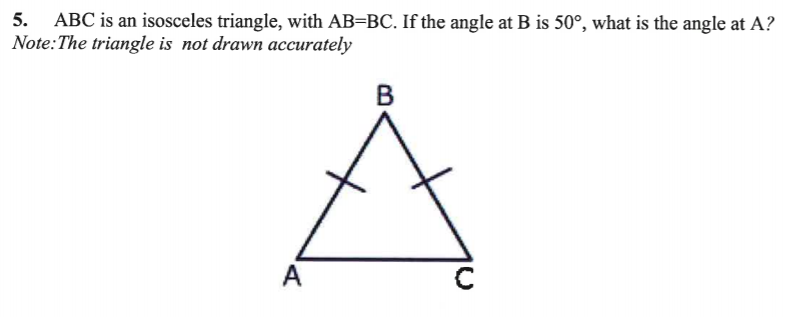
b) 50°
a) 90%
b) 9/24
180 degrees – 45 degrees = 135 degrees
135/360 = 27/72 = 9/24
c) & d) See below
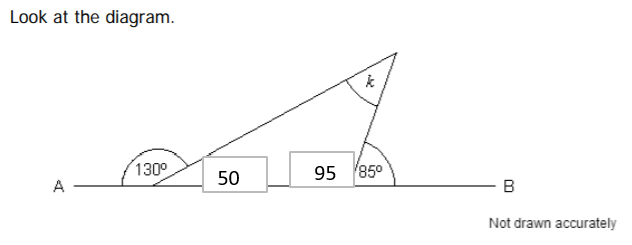
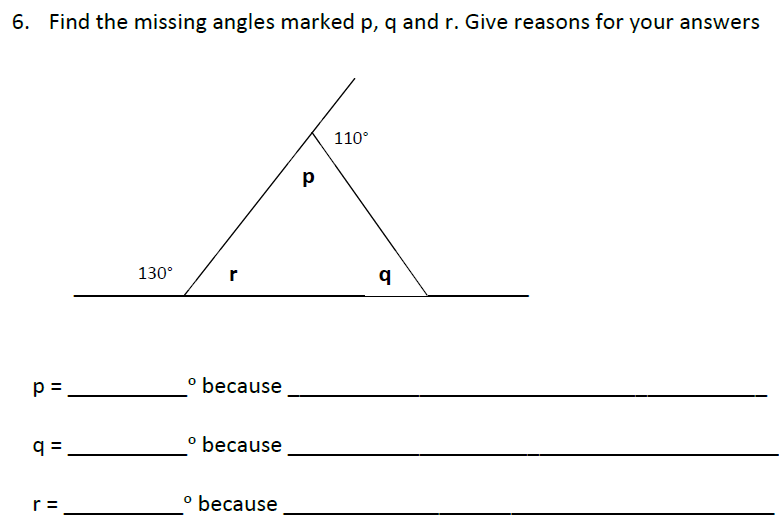
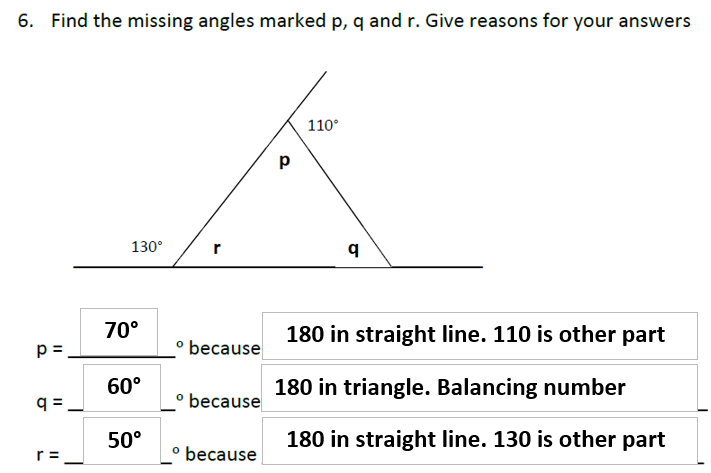
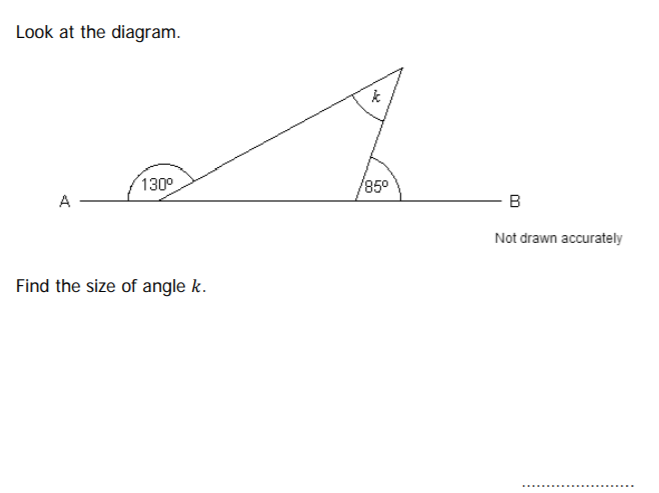
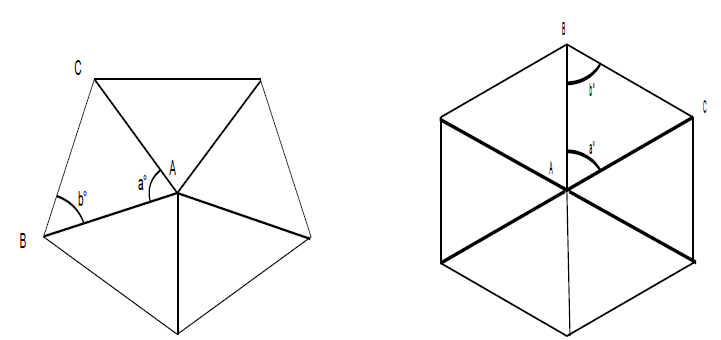
k = 180 -50-95 = 35°
100°
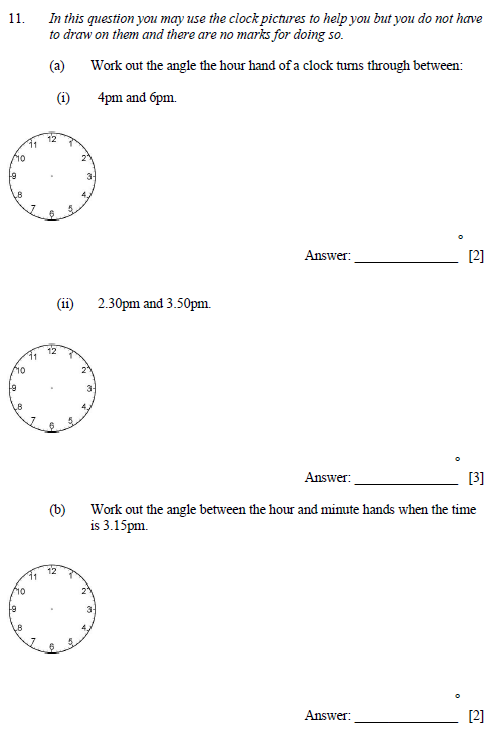
- At 4:40, hour hand will be 2/3rds of the way between 4 and 5
- Minute handle at 40
- So each hour or number on the clock is 30°
- From 4:40 to 5:00 the degree angle is 10°
- From 5:00 to 8 (Which is for 40 mins), the angle is 3 x 30 – 90°
- Add 10 degrees per note 4 and you get 100
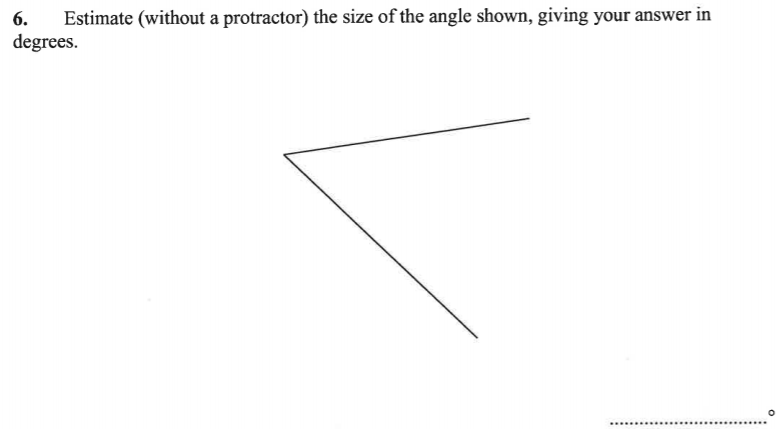
Approximately 40°
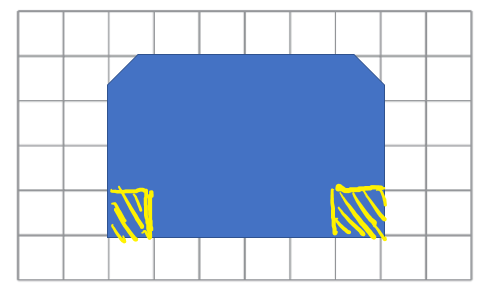
An acute angle
65°
- Triangle = 180°
- 180 – 50 – 130
- 130/2 = 65
B
- 180 – 25 – 107 = 48
E
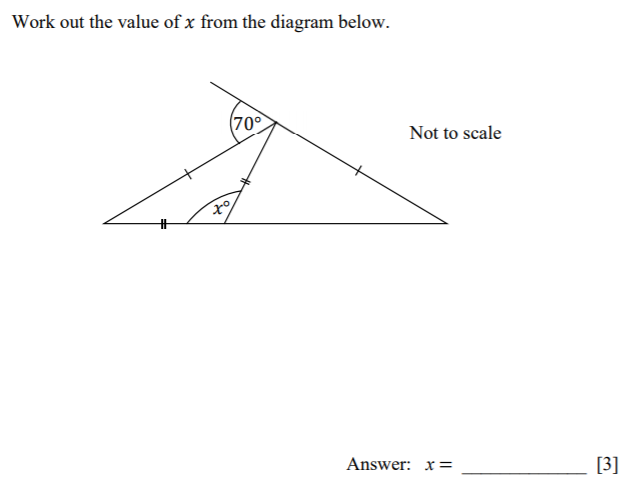
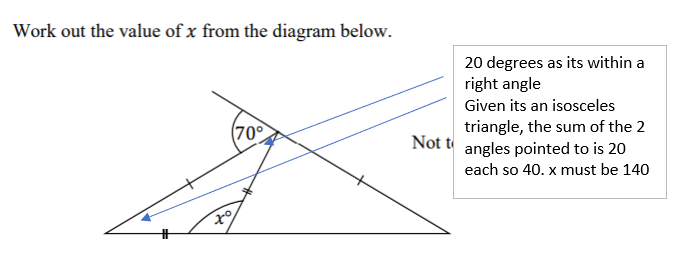
- Isosceles triangles have 2 angles the same
- So, if 30 degrees is one of the angles, then this leaves 150 degrees
- Therefore, 75 degrees is a possible other triangle
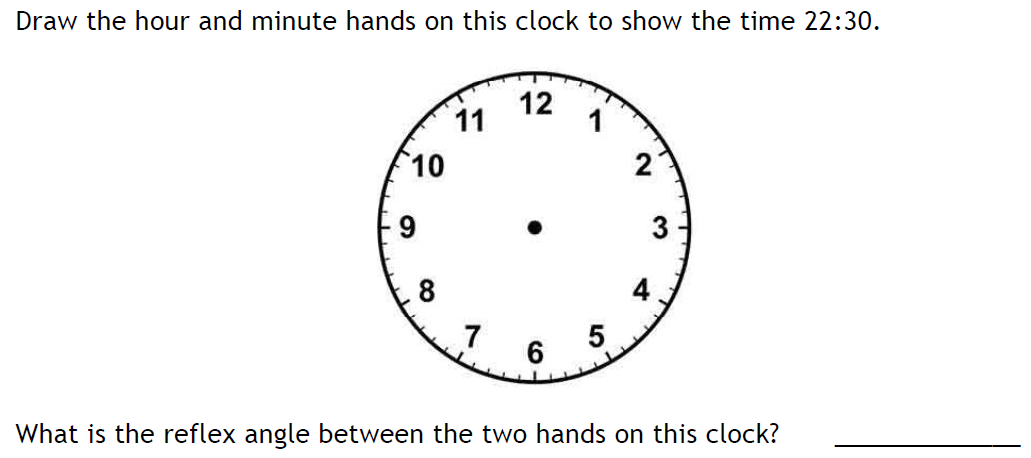
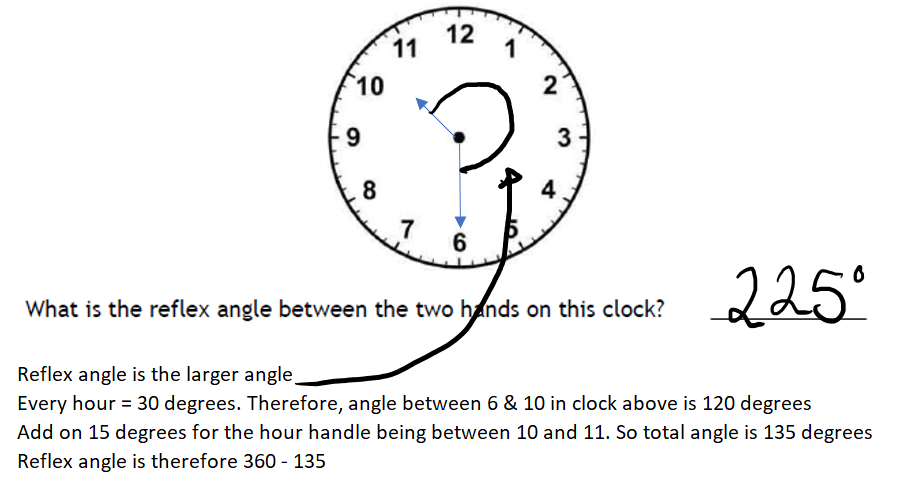
285 degrees
- The internal angle is an actute angle ( Between 0 -90 degrees)
- Therefore, angle r in this case, is a reflex angle (Greater than 180 degrees less than 360 degrees)
- The internal angle is around 75 degrees
- Therefore, r is 360 – 75 = 285 degrees
- The actual size if measured is 70%. Therefore angle r 290. Any number between 280 and 290 for angle r is acceptable
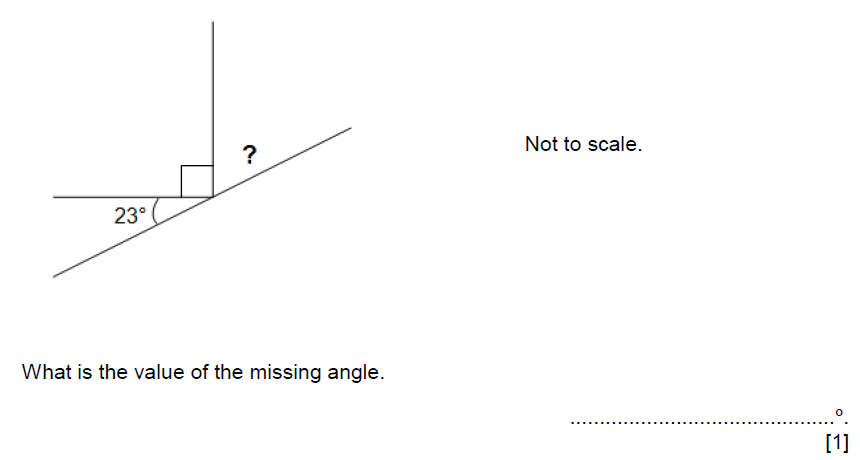
67°
- Angle on a straight line is 180°
- Therefore 180-23-90 = 67
a. 10 seconds
If turn is 360 degrees every 40 seconds, 90 degrees as a right angle would take 1/4 of 40 = 10 seconds
b. 84 turns
In 56 minutes, the sails make 56/1 * 60/40 turns
Again, use of fractions to calculate these types of questions
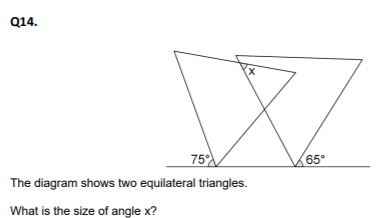
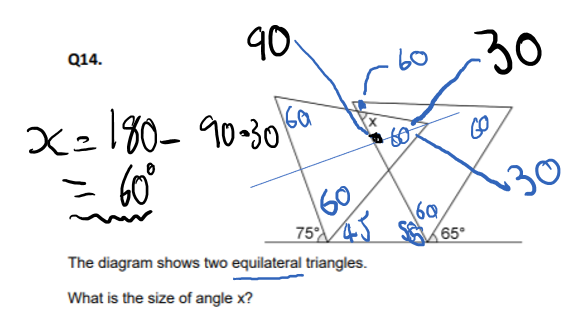
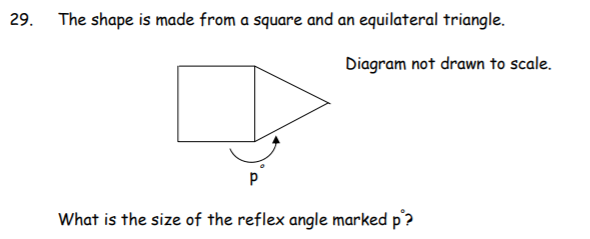
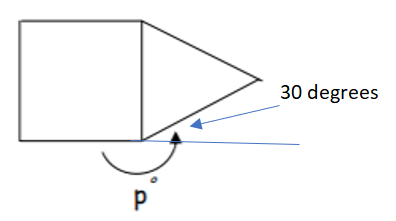
210º
- An equilateral triangle is 60º per inside angle. Therefore, the outside to give a right angle is 30
- In addition , P would be 180 + 3o = 210
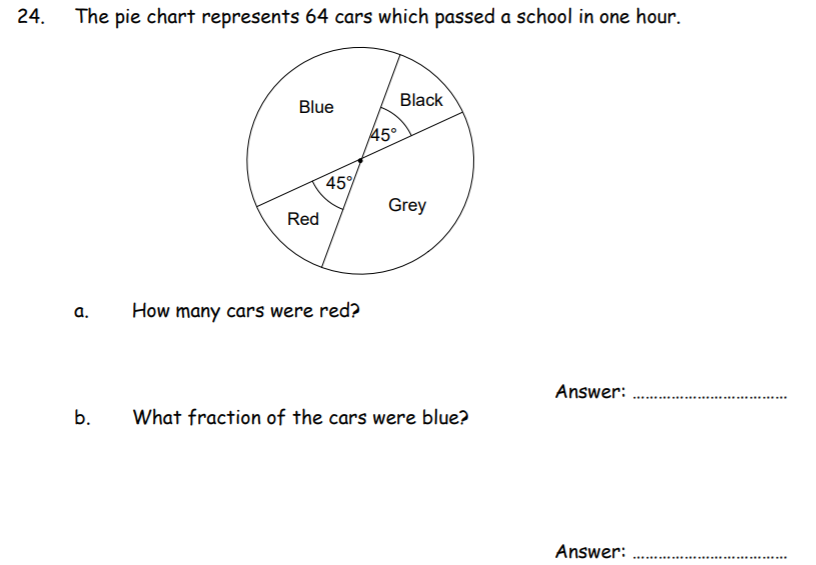
a) 8
-
-
-
- If 64 cars in total, then the following equation will be used to calculate the number of red cars
- 64/1 * 45/360.
- After cross cancellation, this is simplified to:
- 64/1 * 5/40
- Further cross cancellation:
- 8/1 * 1/1
-
-
b) 3/8
- The key here is to remember that the opposite angles when 2 lines cross, create equal angles
- So given Black and Red are 45º each, this gives 90° in total
- So remaining in the circle is 360 – 90 = 270
- Each angle must therefore be 270/2 = 135
- Every 45 degrees = 1/8th. So 135 = 3/8
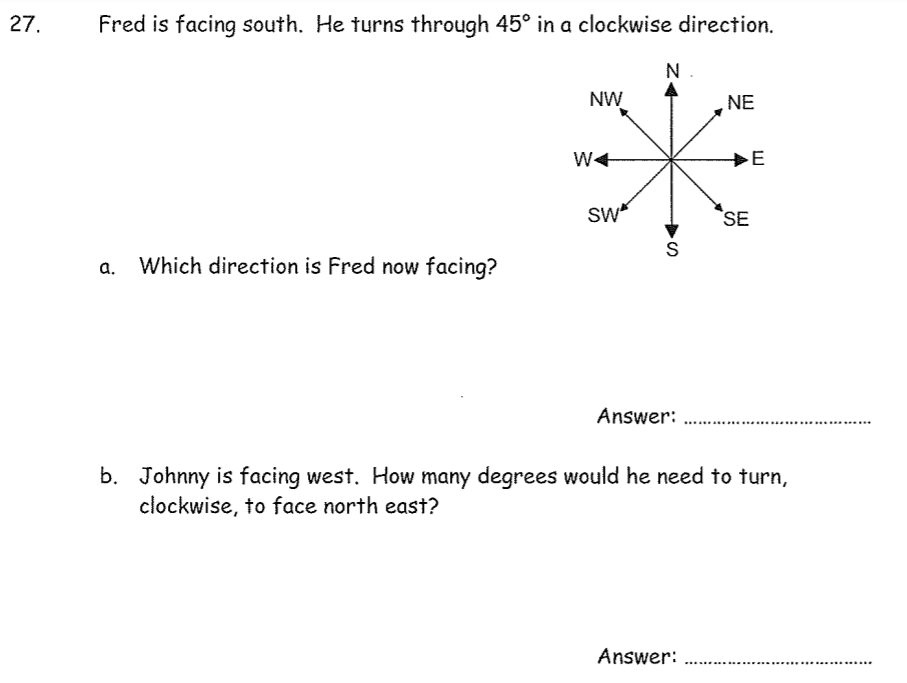
a) NE
b) 135º
90 degrees to face North from West . Then a further 45 degrees to get to NE
c) 225º
- Reflex angle is 360 degrees less the angle from West to NE.
- 360 less 135 = 225
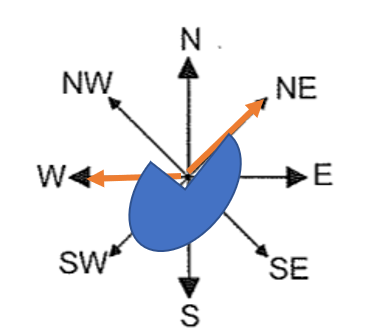
d) SE
- 360 degrees in a circle so of the 495, 360 would bring her back to North
- This leaves 135 degrees. Given 8 markers , each marker is worth 45 degrees
- 135/45 = 3 so she moves by 3 markers
- This takes her to SE
a) 18
- Comedy represents 1/4 of the total pie. This is 25%.
- The pie is worth 72 students in total
- So 1/4 x 72 = 18
b) 50º
- 360 – 90 – 160 – 60 = 50
a) 30º
- Acute means an angle < 90º. So this is when the hour handle is at 12 and minute handle at 1.
- 12 numbers on a regular clock so each one is 30º. (360/12)
- Therefore, at 1 O’Clock, its 30º
b) 15º
- At 6.30pm, the hour handle is exactly in the middle between 6 & 7. The Minute handle is at exactly 6.
- A move from 6 to 7 would be 30º
- So half of this is 15
a) 30º
- Yellow + Purple is a right angle so is 90º
- Therefore, Yellow is 30º
b) 25%
- 100% for the pie chart. Therefore, Red occupies 1/4 of this.
- 100/1 * 1/4
c) 90
-
- 180/360 * 180/1
- This is 180 degrees/360 degrees * 180. The equation above can be simplified and you should always do this
- 1/1 * 90/1
a) octagon
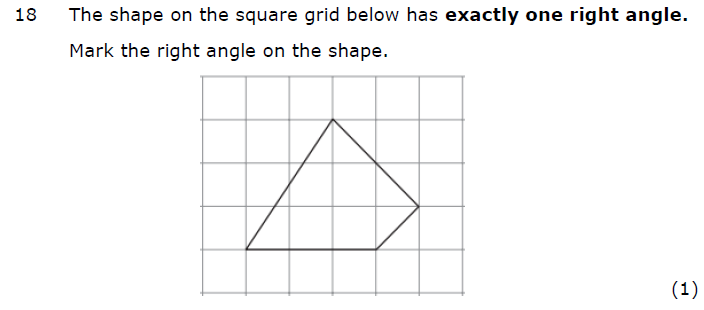
b) obtuse
(greater than 90 degrees)
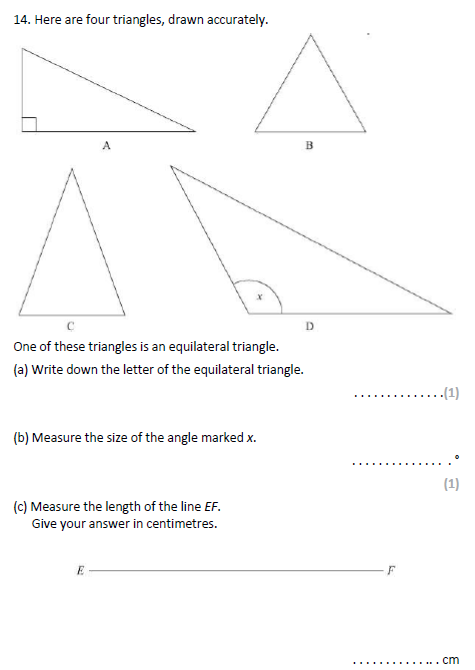
c) i) 3.4cm
c ii) 27.2cm
34mm x 8 = 272mm
Direction you need to turn: Anticlockwise
Angle of turn required: 60 degrees
Like prior word based questions, just break it down 1 sentence at a time:
Start at zero degrees (or think of it as 12 o’clock). 40 degrees clockwise will be to the right
70 degrees anticlockwise will take you a net 30 degrees to the left of zero
90 degrees clockwise turn from there will take you to a net 60 degrees right. So 60 degrees clockwise