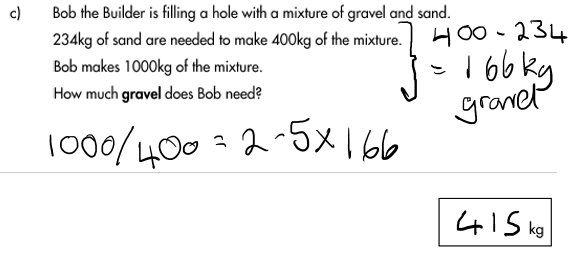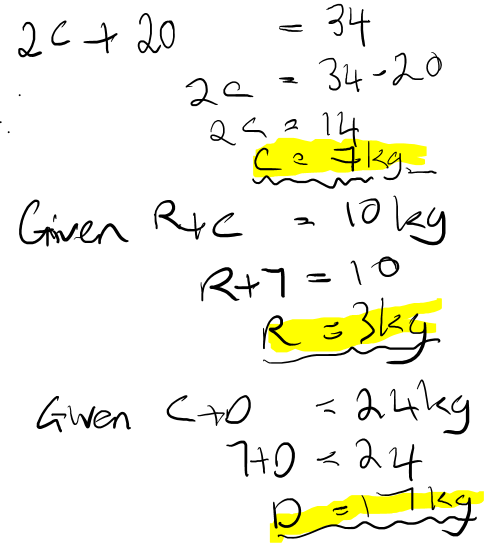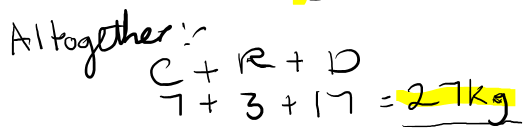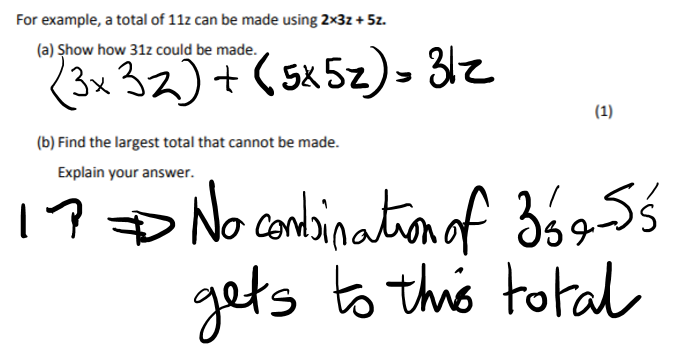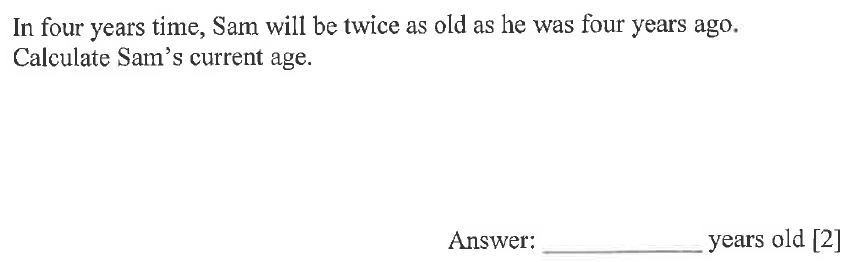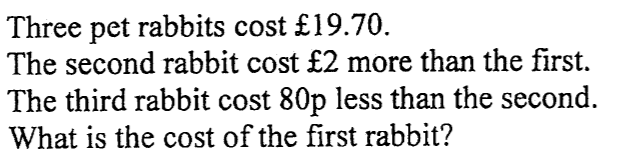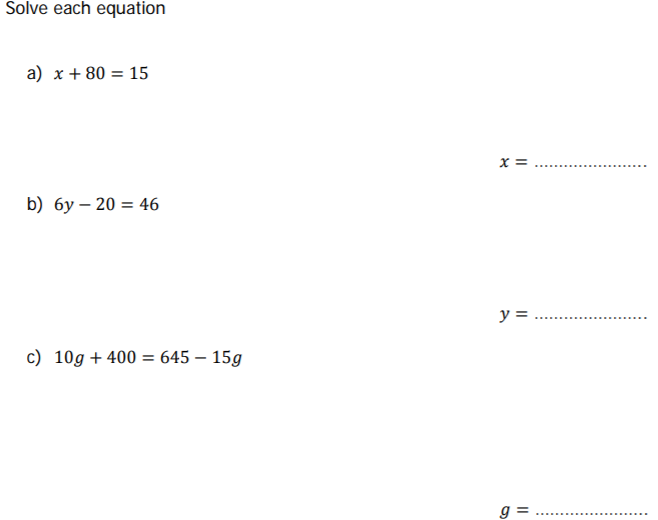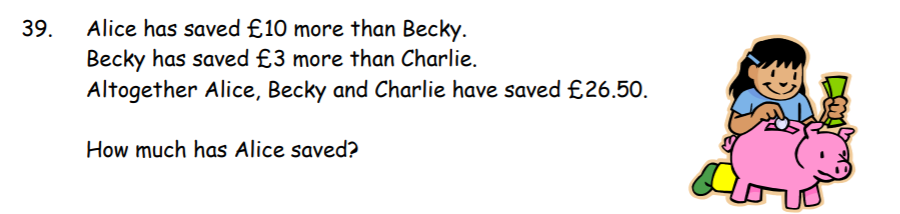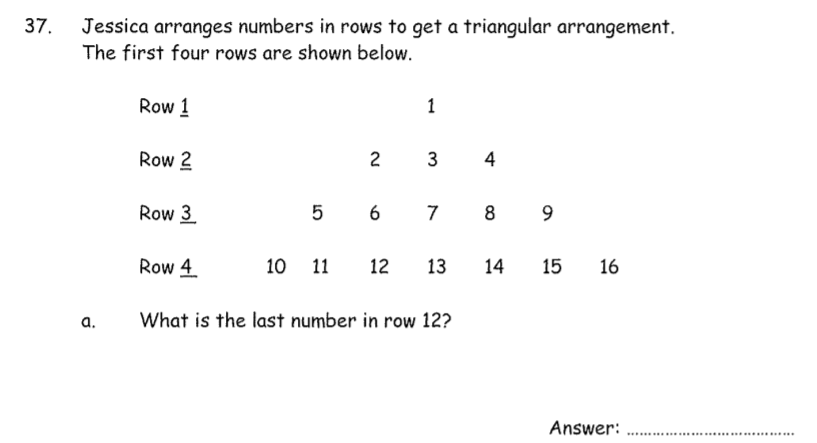algebra

a) Twenty-thousand four hundred

b) -21

A + * by a – is always a –

c) 27

BIDMAS. Brackets first

d) 8

y=16/2 = 8

e)i) x = 7

e)ii) x = 5

You firstly have -x = -5 which is the same as x = 5

f) 6

g) 1:3

a) x = 6

1. 3x + 7 =25
2. 3x=25-7
3. 3x=18
4. x = 6

b) 8

1. 3f – 2g
2. (3*6) – (2*5)
3. 18-10

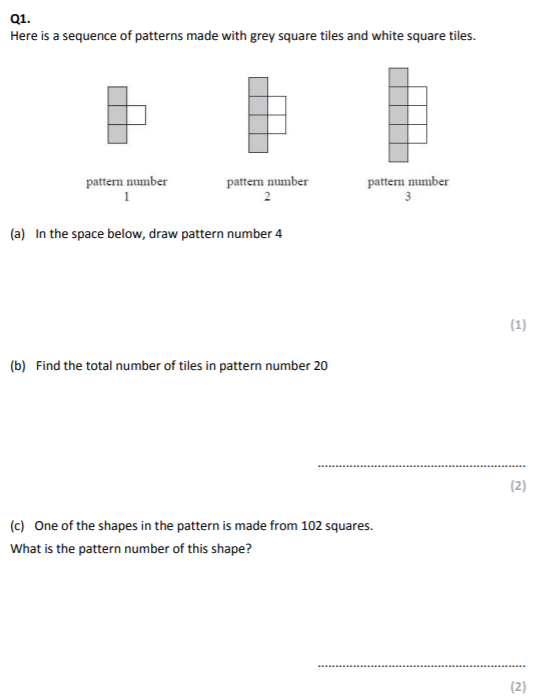
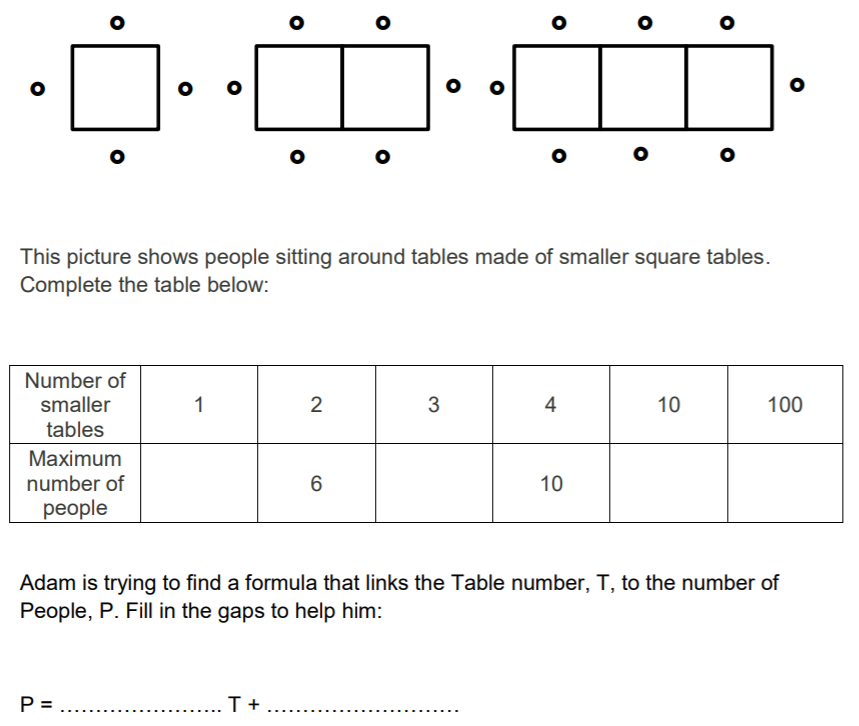
a) See below

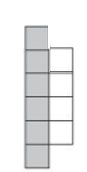
b) 41 Tiles

1. Pattern 1 = 3Grey + 1White = 4 tiles
2. Pattern 2 = 4Grey + 2 White = 6 tiles
3. Pattern 3 = 5Grey + 3 White = 8 tiles
4. So rule is (Pattern number + 1) + Pattern number = Total number of tiles
5. (20+1)+20 = 41

c) 50

1. The pattern starts at 4 tiles and goes up in 2s. But then you have to reduce it by 1 to get to the pattern number. So for Pattern 3, this is 8 tiles. 8 divided by 2 = 4. Less 1 = 3. Confirmed above that this is Pattern 3
2. Therefore, if you have 102 tiles, then this is 51.
3. 51 less 1 = 50

C

15 pens cost £4.65

19 pens cost x

x = (19 * 4.65)/15

C

1. 5((6*9)+(7*3)-(8*6))
2. This gives 5(54+21-48)
3. This gives 5(27)
4. Answer 135

12

1. Can use algebra to solve.
2. 2(x-4) = x+4
3. 2x-8=x+4
4. Rearrange
5. x=12

£5.50

1. A+B+C = £19.70
2. 2nd £7.50, 1st £5.50, 3rd £6.70

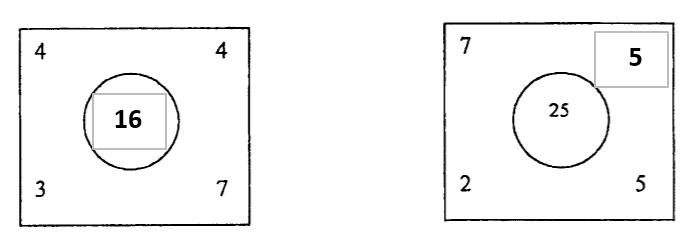
Work backwards for this section….

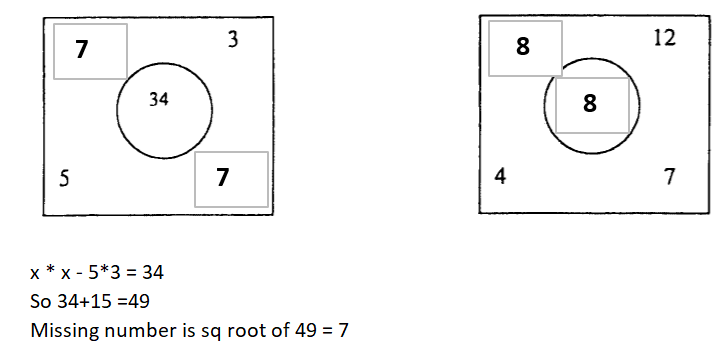
Then BC + A = BC + 4 = 37 so BC = 37 –> B = 3, C = 7. A=4

Checking, 43 + 7 = 50.

a) x=-65

x+80=15

x=15-80

b) y=11

6y=46+20

6y=66

y=11

c) g=9.8

10g+15g = 645-400

25g = 245

g=9 20/25

g = 9.8

a) £27

Cost = ((8×3) + (3×1)) = 24+3 = 27

b) 2 adults. 3 children

Use £25 and work backwards taking off children until you get to a multiple of 8

So £16 would be the number

£25-£16 = £9. So thats 3 children

Leaving £16 so its 2 adults

A = 35p B = 50p

1. 2A + 1B = 1.20
2. 1A + 2B = 1.35
3. Multiply formula in 1 by -2
4. So you get….
5. -4A – 2B = -2.40
6. 1A + 2B = 1.35
7. Add 5 & 6 together
8. -3A = -1.05
9. A = 35p
10. By substitution……
11. 35p + 2B = 1.35
12. 2B = 1.00
13. B = 50p

£1.05

1. 3A + 5O + 2G = £3.02
2. 5A + 7O + 4G = £5.12
3. Therefore, 2A + 2O + 2G = £2.10
4. 1 of each fruit would therefore cost £1.05

250m

1. Use Algebra to solve this. Tom=100t; J=60t. Where t=time
2. 100t=100+60t
3. 40t=100
4. t=2.5
5. 2.5×100=250m

a) 38

(6 x 6) + (6 x 1/3)

b) 5

1. 3 * x = 24
2. (3 x 3) + (3 x ?) = 24
3. 9 + (3 x ?) = 24
4. (3 x ?) = 24 – 9
5. 3 = 15/?
6. ? = 5

c) 4

1. (y * y) + (y * y) = 32
2. y² + y² = 32
3. 2y² = 32
4. y² = 16
5. y =4

a) 12

1. 2A + 1D + 4P = 21
2. So in total 7 parts. Each one is worth 3
3. Preeya must be 12 (3×4)

b) 100cm

1. P + A + D = 300
2. P – D = D – A
3. P + A = 2D
4. 2D + D = 300
5. 3D = 300
6. D = 100

a) £1.20

Just the 2 added together

b) 1 apple = 14p. 1 orange = 16p =30p

Use simultaneous equations approach (x = apple, y=orange):

3x + 1y = 58p

1x + 3y = 62p  multiply by -3 to solve for y

3x + 1y = 58p

-3x – 9y = -186p

-8y = -128p

y =  16p

Use this to solve for a

3x + 16p = 58p

3x = 58p – 16p

3x = 42p

x = 14p

c) 1 apple = 14p.

6

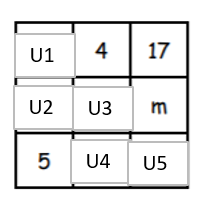
Where “U” stands for Unknown. So Unknown 1 is “U1” etc

U1+4+17 = U2+U1+5

Rearrange:

21 = u2+5

u2=16

Given this, 5+17+u3 = u2+u3+m

22 = 16 + m

m = 6

a) 72

(5+6) * 6

b) 1/2

(1/2 + 1/2) * 1/2

c) 13

(a+2) * 2 = 30

a+2=15

Therefore, rearrange. a=13

d) 5

So (a+a)*a = 2axa=50

a²=25

a=5

Alice = £16.50

1. If their collective total is £26.50, then use Algebra to solve
2. Charlie + 10 + Charlie + 3 + Charlie = £26.50
3. 3Charlie + 16 = £26.50
4. 3Charlie = £10.50
5. Charlie = £3.50
6. So Becky = £6.50
7. So Alice = £16.50

11pence

3p + 1r = 50p

2p + 2r = 56p

Therefore…..

6p + 2r = 100p (x formula 1 by 2)

-2p-2r = -56p

-4p = -44p

=11p

a) 144

The last number in Row 12 will be 144. Spot the pattern which is that its the row number squared to equal the last number

b) 39

Again the patttern. (Row Number x 2) -1  . So for Row 20, it will be 20 x 2 -1

c) 10

Work backwards. Take away 1 and then divide by 2

d) 91

e) 855

a) 5

Applying the rules, = 3 x 3 – 4

b) 6

Working backwards, 32+4 =

So 36 = 6 x 6

c) 9

Slightly trickier. But you need a multiple of 72 with one option being 9

x² – x – 72 = 0

15p per apple

2P + 1M = £1.35 (Formula 1)

1P + 2M = £1.20 (Formula 2)

1P + 1M + 1A = £1.00 (Formula 3)

Take:

4P + 2M = £2.70 (Formula 1 * 2)

1P + 2M = £1.20

Therefore, difference is £1.50 and 3P so each pear costs 50p

If each pear costs 50p, then substituting into formula 1 gives:

£1.00 (2P) + 1M = £1.35

IM = £1.35 – £1.00

1 Mango = 35p

Therefore, given this:

1P + 1M + 1A = £1.00

50p + 35p + 1A = £1.00

1 Apple = 15p

59

1. When you have 2 pages next to each other in a 64 page paper, the 2 pages will add up to 65.
2. Eg 1 & 64 or pages 2 and 63 and so on
3. It will be a page towards the back of the paper. So 6 + x = 65
4. Therefore, rearranging, 59

a) 50

1. Substitute into the “rules” per the example. So this would give (10 x 10) / (1 + 1) = 100/ 2 =50

b) 5

1. First solve (3☺4) = (4×4) / (3+1) = 16/4 = 4
2. Then (4☺5) = (5×5)/ (4+1) = 25/5 = 5

c) 7

1. Have to solve with algebra. 6 ☺ y = (y x y ) / (6 + 1) = y² / 7
2. So y² / 7 = 7. Therefore, rearranging,
3. y² = 7 x 7 . So  y² = 49
4. Therefore , y =7

a) See below

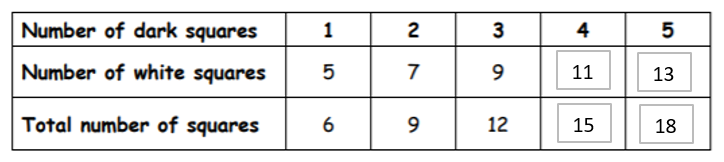
b) 21

1. Its important to recognise the relationship.
2. So with 9 Dark Squares, there would be (2*d) + 3. This is the pattern there for 1 to 5
3. So for 9 it will be (2 * 9) + 3 = 21

c) 10

1. You have to work backwards given W=(2*d) + 3
2. Given w=23, 23 = (2d) + 3. Rearrange to 23-3 = 2d
3. 20=2d. So d must equal 10

d) 31

1. If a pattern has 45 squares in total so again the trick is to recognise the pattern that derives the total
2. First calculate dark. So Dark = (Total/3 – 1 ). = 45/3 -1 = 14
3. Given this, white must equal (2*d) + 3 = 31

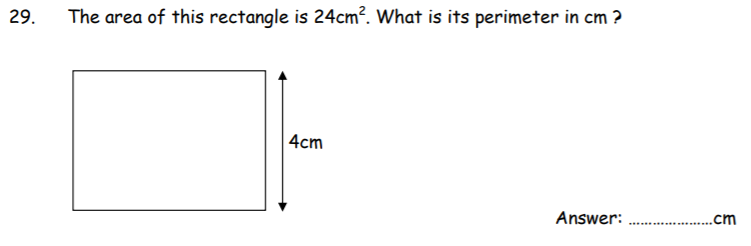
20cm

1. Very Standard style question where you are given the area and have to work out the perimeter.
2. x * 4 = 24cm² would give the area. So re-arrange this. Where x = Length. 4 is Width
3. 24/4 = x
4. x = 6
5. So if x = 6, the solution is [(2 * 6) + (2 * 4) ]

a) 14

(4 * 5)- (2 * 3). Just substitute the numbers in the formula remembering to add brackets

b) 7

Rearrange the formula. k – (2*3) = 29

29 – – 6 = k

35 = k. Therefore, given you have to multiply by 5 to get to k, k must be 7

c) -3

Calculate as per part a by substituting values into the formula remembering to rearrange

d) 13

7

jj = jupiterian jellyfish

Summarise the question in algebra format. It will make it easier to solve. Total Tentacles:

(jj x 25 ) + (20 – jj) * 8 = 279

25jj + 160-8jj = 279

17jj + 160 = 279

17jj = 119

jj = 7

a) Number of packets of apples = 4

Oranges = x. Apples = y

5(3x) + ?(4y) = 31

15 + ?(4y) = 31

?(4y) = 16

?y = 16/4

Number of packets of apples = 4

b)  3 packets oranges and 5 packets of apples

3y + x = 29.  = 12 + 3 = 15 pieces of fruit. He needs a further 14. Therefore, the combination would be a further 2 packets of oranges and 2 packet of apples. This equals 5 packets oranges and 3 packets apples

c) 16

Given apples = y,

40 pieces

4y + 3(11-y) = 40

y+33 = 40

y = 7. Therefore, with 4 apples per pack, thats 28 apples. You therefore have 3 oranges per pack and in total 12 oranges. Therefore, apples > oranges = 16

a) 5

10T = 18 papers per teacher over the 3 hour timeframe. Which equals 6 papers per teacher per hour

To mark 90, requires total of 15 hours. Therefore 5 teachers

10/180 * T/90 = (10*90)/180 = T. T=5

b) 5

3 x 10 = T x 5 = 30/5

c) 120

6 papers per hour * 20 Teachers = 120 papers

a) See below

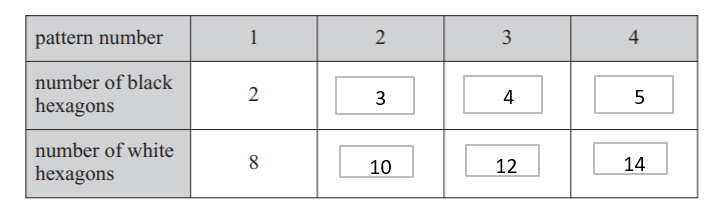
b) 14

There is always one more hexagon than the pattern number

c) 26

The relationship is that you multiply the pattern number by 2 and then add 6 to get the number of white hexagons. So 2pn + 6. (2*10) + 6

d) 23

Work backwards. 50 white less 6 = 44. Divide by 2 gives you 22. So this represents the number of black hexagons

Given the rule in b), it has to be 23

a) £2.60

Questions which mention something is “twice as much as something else” or a multiple of something else, requires a few possible approaches. One is to use ratios. So Cake:Drink is 2:1

There are 3 parts altogether. So £3.90/3  = £1.30 per part

Cake is 2 parts so cost is £2.60

b) £1.45

Tea + Fizzy drink = £2.60

Fizzy drink 30p more. So £2.60/2 = £1.30 if it was an equal price. To get a 30p difference, you add 15p to one and take 15p to the other. So Fizzy drink will cost £1.45 and revised cost for Tea will be £1.15

c) 91p

A+B = 57p

B+P = 56p

A+P = 69p

Therefore, there are 2 apples, 2 bananas and 2 pairs. If you add all of the above together and x2, you get £1.82

Divide by 2 gives 91p

a) 18p

1a+2o+3p = £2.10

o + p =64p

3o + 3p = £1.92

Use simultaneous equations

1a+2o+3p = £2.10

less 3o + 3p = £1.92

Difference is therefore 18p

b) 12

(4 x cars) + 2 x (27 – cars)  = 78

4c + 54 – 2c = 78

2c + 54 = 78

2c = 24

c = 12

12

The best way to solve this question is with the use of Algebra. In fact many maths questions where they have someone or something being “X” times more or less than the other, Algebra comes in handy. So lets solve….

2Harsha=1Ravi

2Ravi=1Harpreet

If 42 sweets altogether, then lets work out the total number of “shares” of sweets:

4Harsha+2Ravi+1Harpreet

In the above, you start with Harpreet as being 1 share (or x if you like) and then work through to Harsha

The objective is to get to the number of “shares” to see how many portion you divide the sweets between. Its 7 times

So 42/7 means each share of sweets is worth 6.

Ravi gets 2 shares so he gets 12

19

Simplest approach is to convert this to an algebra format question

So, since the number is doubled, let this equal 2x

41-2x=3

Then rearrange as per normal

-2x=3-41

2x=38

x=19